Complex numbers z, having the same modulus |z| = r, obviously correspond to points of the complex plane located on a circle with center (0;0) and radius r. If |z|≠0, then there are infinitely many complex numbers with this modulus. And there is only one complex number z=0 that has a modulus equal to zero.
Arguments of a complex number
It is geometrically obvious that the complex number z≠0, z=a+bi will be uniquely determined if, in addition to the modulus, we specify, for example, the value of the angle φ between the positive direction of the X axis and the vector z:
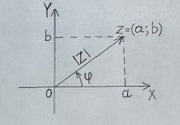
The argument of the complex number z≠0 is the value of the angle between the positive direction of the X axis and the z vector, where the value of the angle is considered positive if the counting is counterclockwise, and negative if clockwise.
Obviously, the argument of a complex number is not uniquely defined, since any angle that differs by a multiple of 2π will also be an argument of the number z, that is, each complex number has an infinite set of arguments.
Thus, specifying the modulus and the argument uniquely defines a complex number. For the number z=0, the argument is not defined, but only in this case the number is set by its modulus. The argument of a complex number, unlike a modulus, is defined ambiguously.
The real and imaginary parts of a complex number z=a+bi, as the figure shows, are expressed through its modulus r=|z| and argument φ as follows:
a=rcosφ; b=rsinφ.
Let's rewrite this system as follows:
cosφ=a/r; sinφ=b/r. ⇔ cosφ=a/√(a2+b2); sinφ=b/√(a2+b2).
Obviously, there are an infinite number of solutions φ to these equations, since any two arguments of a complex number differ by a multiple of 2π. The entire set of arguments is denoted by arg(z) or arg(a+bi). If one particular argument is meant, it is usually denoted by the letter φ.
Examples of finding the arguments of a complex number
Example 1.
Find the arguments of a complex number i.
Solution.
a+bi = i ⇔ a=0; b=1 ⇔ r=√(0+1)=1; cosφ = a/r = 0; sinφ = b/r = 1. These values of cosine and sine correspond to the value of the argument φ=π/2.
⇔ r=1; φ=π/2.
Thus, arg(z) = π/2+2πk, where k is an arbitrary integer.
Answer: π/2+2πk, k∈Z.
Example 2.
Find the arguments of a complex number -1+i.
Solution.
a+bi = -1+i ⇔ a=-1; b=1 ⇔ r=√(1+1)=√2; cosφ = a/r = -1/√2; sinφ = b/r = 1/√2 ⇔ r=√2; φ=3π/4.
Thus, arg(z) = 3π/4+2πk, where k is an arbitrary integer.
Answer: 3π/4+2πk, k∈Z.
Example 3.
Find the arguments of a complex number -1-√3i.
Solution.
a+bi = -1-√3i ⇔ a=-1; b=-√3 ⇔ r=√(1+3)=2; cosφ = a/r = -1/2; sinφ = b/r = -√3/2 ⇔ r=2; φ=-2π/3.
Thus, arg(z) = -2π/3+2πk, where k is an arbitrary integer.
Answer: -2π/3+2πk, k∈Z.
The arguments of a complex number can be found in another way. From the figure it follows that each of the arguments satisfies the equation:
tgφ=b/a.
This equation has more solutions than the system of equations we used earlier. But selecting the right solutions is not difficult, since the algebraic form of the complex number immediately tells us in which quadrant of the complex plane the number is located.
xample 4.
Find the arguments of a complex number -√3+i.
Solution.
a+bi = -√3+i ⇔ a=-√3; b=1 => tgφ = b/a = -1/√3 => φ=-π/6.
But since the number z=-√3+i is located in the second quadrant of the complex plane, its arguments will be numbers φ=5π/6+2πk, k∈Z.
Answer: 5π/6+2πk, k∈Z.
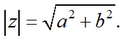 It is obvious that conjugate complex numbers have equal modules and the following relation is valid for them::
It is obvious that conjugate complex numbers have equal modules and the following relation is valid for them::
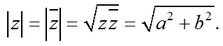 For a real number z = a + 0*i, the modulus coincides with the absolute value of the number a.
For a real number z = a + 0*i, the modulus coincides with the absolute value of the number a. The argument of the complex number z≠0 is the value of the angle between the positive direction of the X axis and the z vector, where the value of the angle is considered positive if the counting is counterclockwise, and negative if clockwise.
Obviously, the argument of a complex number is not uniquely defined, since any angle that differs by a multiple of 2π will also be an argument of the number z, that is, each complex number has an infinite set of arguments.
The argument of the complex number z≠0 is the value of the angle between the positive direction of the X axis and the z vector, where the value of the angle is considered positive if the counting is counterclockwise, and negative if clockwise.
Obviously, the argument of a complex number is not uniquely defined, since any angle that differs by a multiple of 2π will also be an argument of the number z, that is, each complex number has an infinite set of arguments.