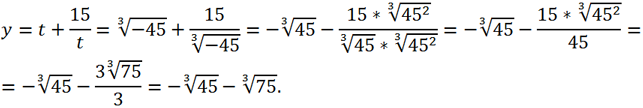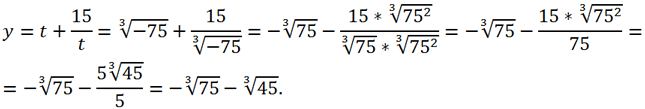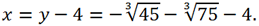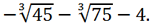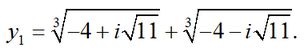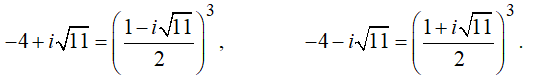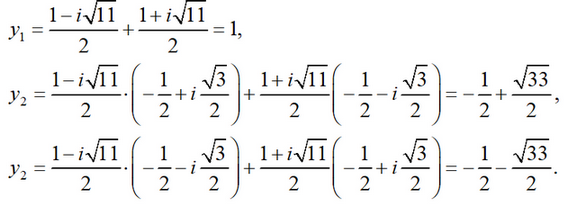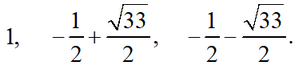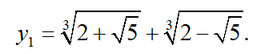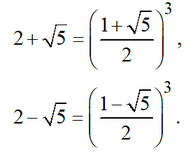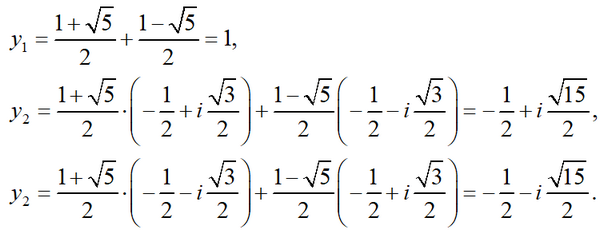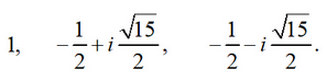As is known, the n-th root of a complex number
z,
z = r *(cosφ + isinφ)
has n complex values
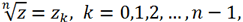
where
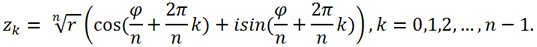
Therefore,
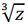
has 3 values z
1, z
2, z
3, where
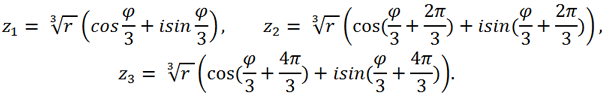
There are two cubic roots in the Cardano formula, and their values must be combined according to the following rule: for each of the three values of the first cubic root
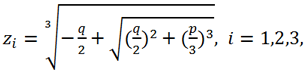
the value of the second cubic root is taken so
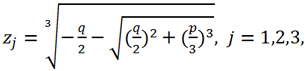
that the ratio is fulfilled z
i*z
j = -
.
Therefore, out of 9 combinations of cubic roots, only 3 are suitable for us. Let t
1 and t
2 be a pair of suitable values of cubic roots, i.e. t
1*t
2=-p/3.
Let's denote

Since t
1g
1*t
2g
2=t
1*t
2=-p/3 и t
1g
2*t
2g
1=t
1*t
2=-p/3,
then the two remaining pairs of cube root values will be t
1g
1, t
2g
2 and pair t
1g
2, t
2g
1.
Thus, we obtain Cardano's formulas for the three roots of the canonical cubic equation:
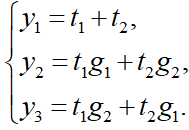
To avoid such a combination of values of different cubic roots, you can use the formula
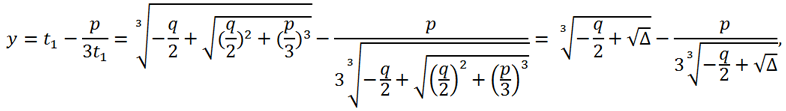
or, what is the same thing,
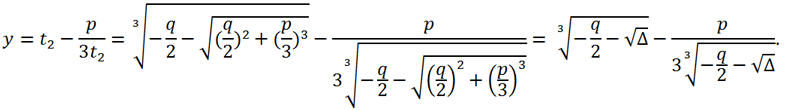
Each value of y found by the Cardano formula corresponds to the solution of the original equation x = y - b/(3a).
If p and q are real numbers, then depending on the value of the discriminant Δ a cubic equation can have either 3 real roots, (Δ <0), or 1 real root and two complex conjugates (Δ > 0), or 2 real roots (Δ=0) - one of them is simple, the other is of multiplicity 2, or one real root of multiplicity 3 (Δ=0, p=q=0). Let's consider all these cases.
1) Δ <0 => 3 real roots:

where
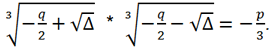
If we omit the intermediate calculations, the final formulas for the three real roots of the canonical equation can be represented as

where
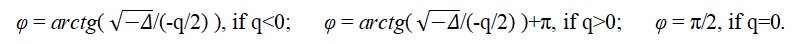
Here is another form of writing the roots of the canonical equation. Let
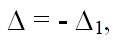
where
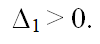
Then the formulas for the three real roots of the canonical equation can be represented as:
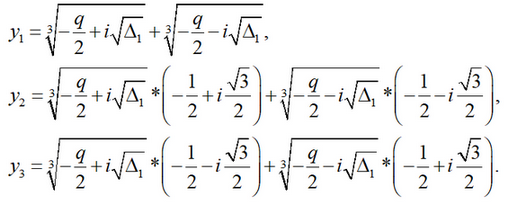
Let's write down the formulas for the roots of the original equation:
x1 = y1 - , x2 = y2 - , x3 = y3 - .
2 ) Δ > 0 => 1 real root and two complex conjugates:
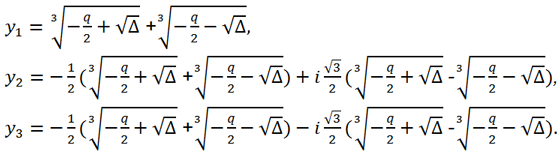
The formulas for the roots of the original equation are the same as in the previous case
x1 = y1 - , x2 = y2 - , x3 = y3 - .
3 ) Δ=0 => 2 real roots (one is simple, the other is of multiplicity 2):
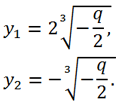
Therefore, x
1 = y
1 -
, x
2 = y
2 -
. In this case, the original equation has one simple root (x
1), and another of multiplicity 2 (x
2=x
3).
If Δ=0 and p=q=0, then the canonical equation has only one root y
1=0. Accordingly, the original equation will have a single root of multiplicity 3
x = -.
If a cubic equation has an integer or rational root, then, of course, the easiest way is to find this root by selection, then reduce the original equation to a quadratic one by division. If there are no rational roots, then only the Cardano formula can help find a solution.
The practical use of the Cardano formula for solving cubic equations is extremely difficult due to cumbersome calculations. But in special cases, it is quite easy to do this, for example, for the first case (Δ < 0) when q = 0 to find three real roots, or for the third case. (Δ = 0). For the second case, when Δ > 0 , the formulas for the roots of the cubic equation can always be written out. Thus, the application of Cardano's formula is justified if the equation does not have rational roots.
Let us consider the application of Cardano's formula to solving cubic equations using examples.
Examples of using the Cardano formula to solve cubic equations
Example 1.
Solve the equation x
3 + 6x
2 + 3x - 10 = 0.
Solution.
This equation can be easily solved without using the Cardano formula. It is easy to pick up the root x = 1. By dividing the left side of the equation by x - 1 using Horner's scheme, we obtain
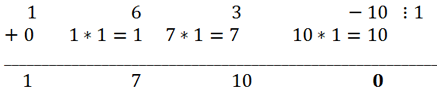
Therefore, x
2 + 7x + 10 = 0. Solving this quadratic equation, we get
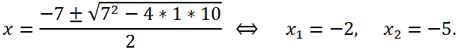
Now let's find the roots of the original equation using Cardano's formula. For this equation a = 1, b = 6, c =3, d = -10. Replacing a variable x = y - b/(3a) = y - 6/3 = y - 2
brings the original equation to the form y
3 + py + q = 0, where
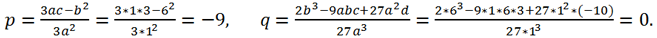
Let's calculate the discriminant of this equation
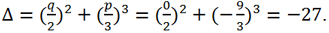
Since Δ <0 => the canonical equation has 3 real roots. Since q = 0 => φ =
=>
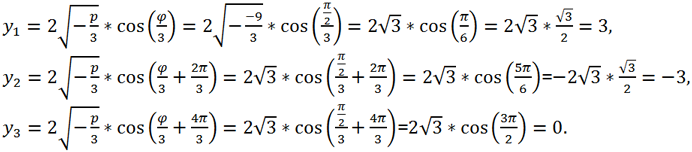
Then for the roots of the original equation we get:
x
1 = y
1 - 2 = 3 - 2 = 1,
x
2 = y
2 - 2 = -3 - 2 = -5,
x
3 = y
3 - 2 = 0 - 2 = -2.
Answer: -5, -2, 1.
Example 2.
Solve the equation x
3 + 3x
2 + 4x + 2 = 0.
Solution.
For this equation a = 1, b = 3, c =4, d = 2. Replacing the variable x = y - b/(3a) = y - 3/3 = y - 1 brings the original equation to the form y
3 + py + q = 0, where
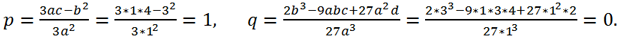
Let's calculate the discriminant of this equation
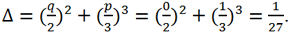
Since Δ >0 => the canonical equation has 1 real root and two complex conjugates:
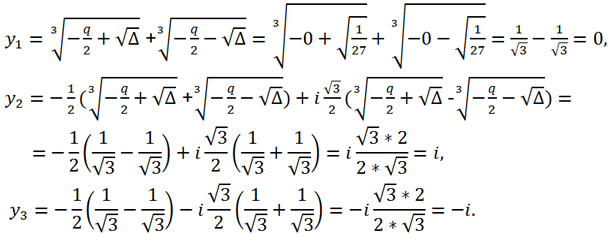
Then for the roots of the original equation we get:
x
1 = y
1 - 1 = 0 - 2 = -1,
x
2 = y
2 - 1 = i - 1 = i - 1,
x
3 = y
3 - 1 = -i - 1 = -i - 1.
Answer: -1, -1+i, -1-i.
Example 3.
Solve the equation x
3 + 12x
2 + 36x + 32 = 0.
Solution.
For this equation a = 1, b = 12, c =36, d = 32. Replacing the variable x = y - b/(3a) = y - 12/3 = y - 4 brings the original equation to the form y
3 + py + q = 0, where
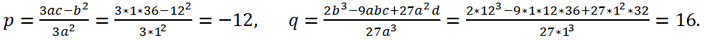
Let's calculate the discriminant of this equation
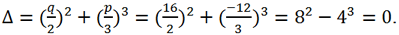
Since Δ = 0 => the equation has 2 real roots:
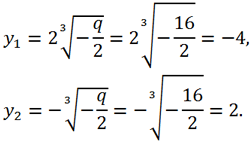
Then for the roots of the original equation we get:
x
1 = y
1 - 4 = -4 - 4 = -8,
x
2 = y
2 - 4 = 2 - 4 = -2.
Answer: -8, -2.
Example 4.
Solve the equation x
3 + 9x
2 + 9x - 137 = 0.
Solution.
For this equation a = 1, b = 9, c =9, d = -137. Replacing the variable x = y - b/(3a) = y - 9/3 = y - 3 brings the original equation to the form y
3 + py + q = 0, where
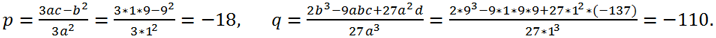
Let's calculate the discriminant of this equation
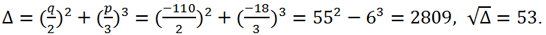
Since Δ >0 => the canonical equation has 1 real root and two complex conjugates:
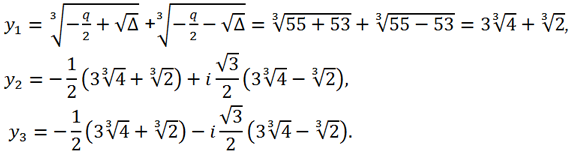
Then for the roots of the original equation we get:
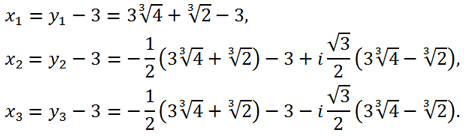 Answer:
Answer: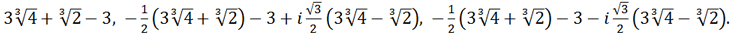 Example 5.
Example 5.
Solve the equation x
3 + 18x
2 + 90x + 50 = 0.
Solution.
For this equation a = 1, b = 18, c =90, d = 50. Replacing the variable x = y - b/(3a) = y - 18/3 = y - 6 brings the original equation to the form y
3 + py + q = 0, where
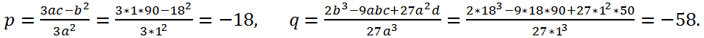
Let's calculate the discriminant of this equation
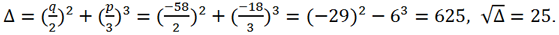
Так как Δ > 0 => the canonical equation has 1 real root and two complex conjugates:
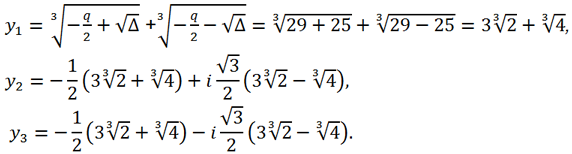
Then for the roots of the original equation we get:
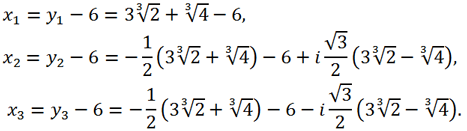 Answer:
Answer: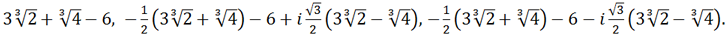
Since it is quite difficult to remember the intermediate formulas for finding the roots of a cubic equation using Cardano's formula, you can simply repeat the derivation of Cardano's formula for this equation. Let's consider the corresponding example.
Example 6.
Find the real roots of the equation x
3 + 12x
2 + 3x + 4 = 0.
Solution.
For this equation a = 1, b = 12, c = 3, d = 4. Let's replace the variable x = y - b/(3a) = y - 12/3 = y - 4:
(y - 4)
3 + 12(y - 4)
2 + 3(y - 4) + 4 = 0
<=> y
3 - 12y
2 + 48y - 64 + 12y
2 - 96y + 192 + 3y - 8 = 0 <=>
<=> y
3 - 45y + 120 = 0.
Therefore, p = -45, q = 120, Δ = (60)
2 - (15)
3 = 225 >0. So the original equation has one real root.
Now let's make the following variable substitution y = t - p/(3t) = t + 45/(3t) = t + 15/t. We get
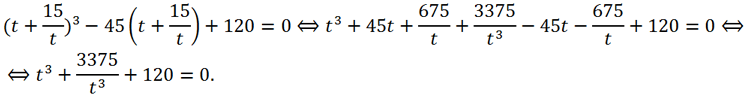
We multiply this equation by t
3 and get a quadratic equation with respect to t
3: t
6 + 120t
3 + 3375 = 0.
Hence,
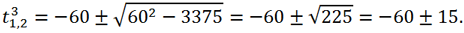
Then
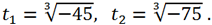
Now you can find y by the formula y = t +
.
Instead of t, you can substitute either
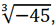
or
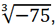
the result will be the same:
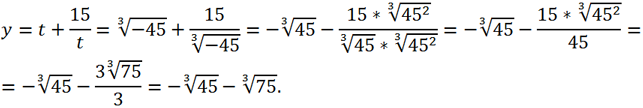
Or
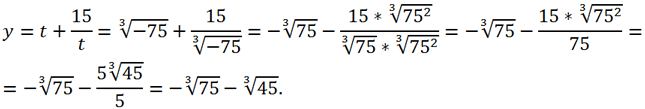
Thus, the real root of the original equation is equal to
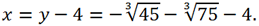 Answer:
Answer: 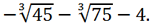
Let's consider two examples of using the Cardano formula when the cubic equation has a rational root, but this root is difficult to see in the number obtained by the Cardano's formula.
Example 7.
Solve the equation y
3 - 9y + 8 = 0.
Solution.
For this equation p = -9, q = 8, Δ = (4)
2 + (-3)
3 = -11 <0. Therefore, the original equation has 3 real roots. By simple selection it is easy to find a root equal to 1. Let's see what Cardano's formula gives us in this case:
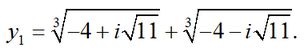
It's almost impossible to see 1 in this number unless you know that
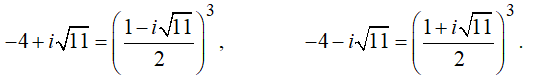
Then for the three real roots of the equation we have
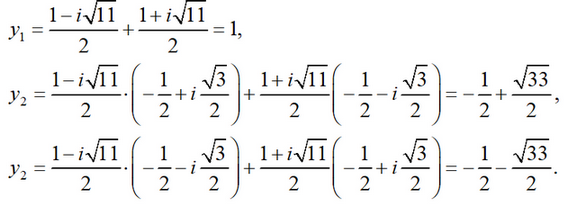 Answer:
Answer: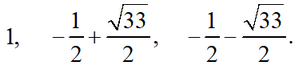 Example 8.
Example 8.
Solve the equation y
3 + 3y - 4 = 0.
Solution.
For this equation p = 3, q = -4, Δ = (-2)
2 + (1)
3 = 5 >0. Therefore, the original equation has 1 real root and two complex conjugates. In this example, as in the previous one, there is root 1 among the roots. Cardano's formula gives the number:
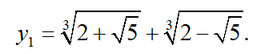
Here you also need to know that
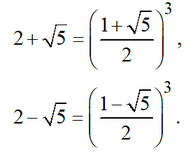
Then for the three roots of the equation we have
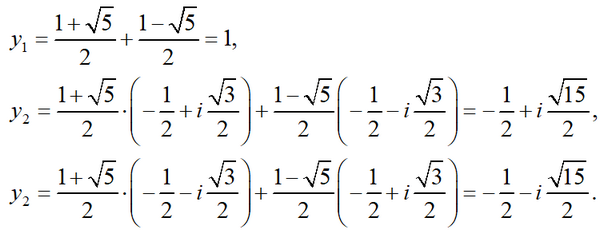 Answer:
Answer: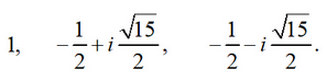
 Another variable replacement y = t - p/(3t) leads a three-term cubic equation to the form
Another variable replacement y = t - p/(3t) leads a three-term cubic equation to the form 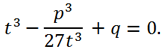
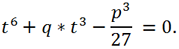 The last equation is a quadratic equation with respect to t3, its roots can be written out explicitly:
The last equation is a quadratic equation with respect to t3, its roots can be written out explicitly: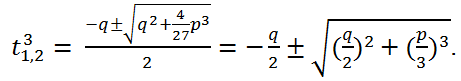
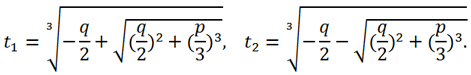
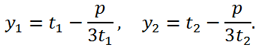 Although the expressions for y1 and y2 look different, they are the same numbers. Let's transform them as follows. In the expression for y1 we multiply both the numerator and the denominator of the fraction
Although the expressions for y1 and y2 look different, they are the same numbers. Let's transform them as follows. In the expression for y1 we multiply both the numerator and the denominator of the fraction 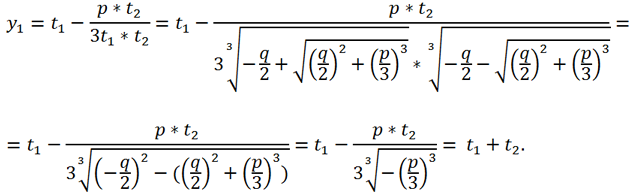
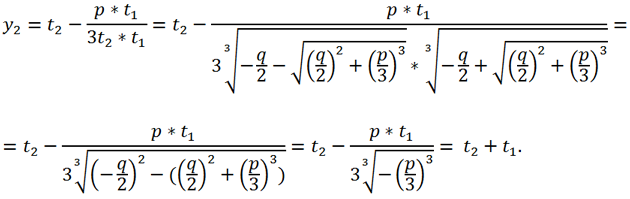
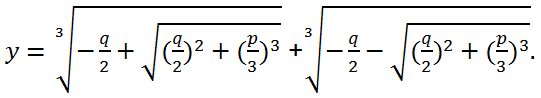
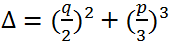 is called the discriminant of the third-degree equation y3 + py + q = 0.
is called the discriminant of the third-degree equation y3 + py + q = 0.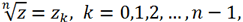 where
where 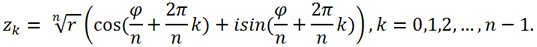 Therefore,
Therefore, 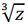 has 3 values z1, z2, z3, where
has 3 values z1, z2, z3, where 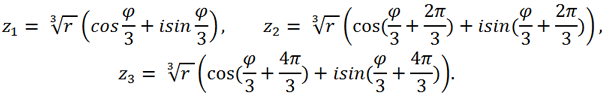
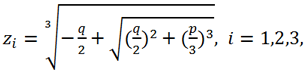 the value of the second cubic root is taken so
the value of the second cubic root is taken so 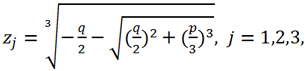 that the ratio is fulfilled zi*zj = -
that the ratio is fulfilled zi*zj = -
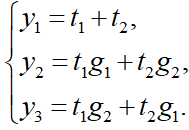
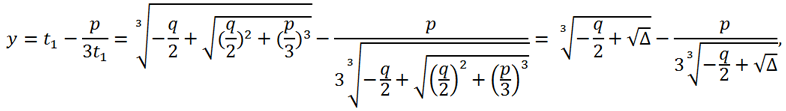
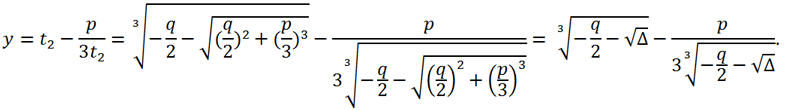
 where
where 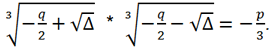
 where
where
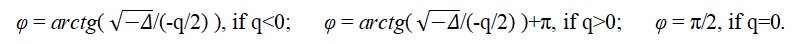 Here is another form of writing the roots of the canonical equation. Let
Here is another form of writing the roots of the canonical equation. Let 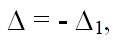 where
where 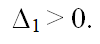 Then the formulas for the three real roots of the canonical equation can be represented as:
Then the formulas for the three real roots of the canonical equation can be represented as:
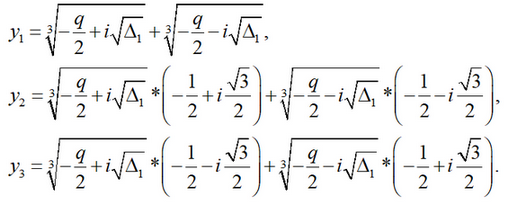
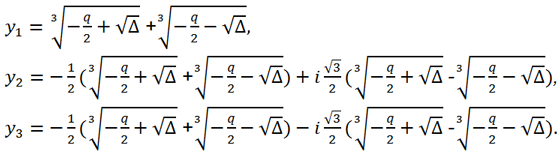
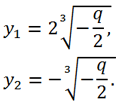
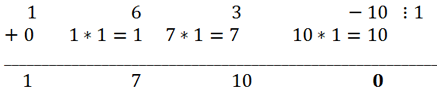
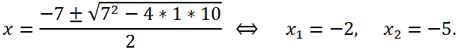
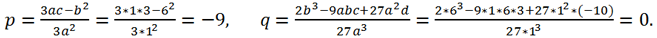
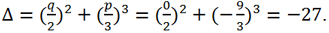
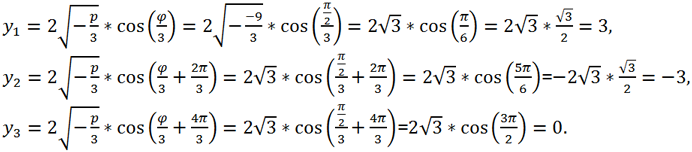
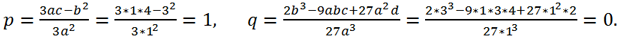
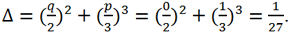
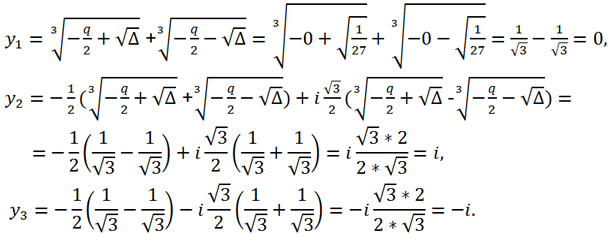 Then for the roots of the original equation we get:
Then for the roots of the original equation we get: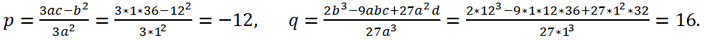
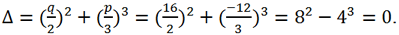
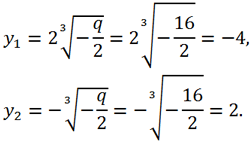
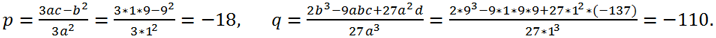
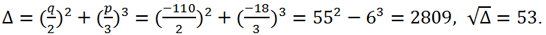
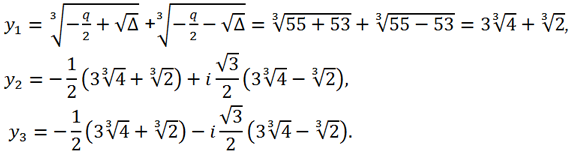
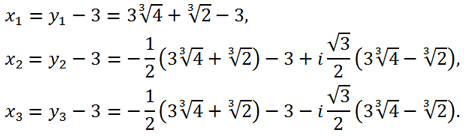
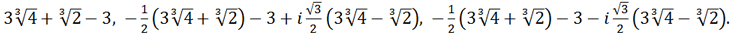
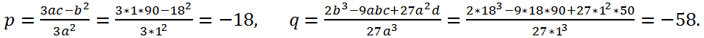
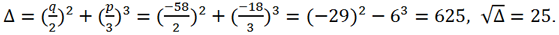
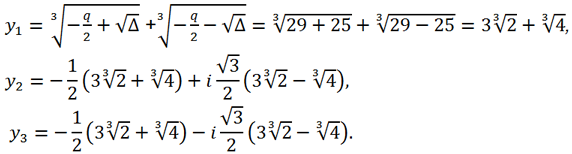
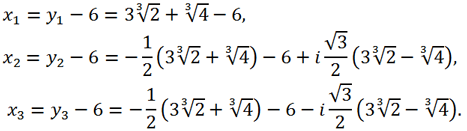
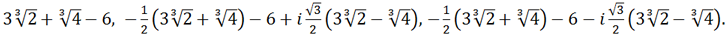
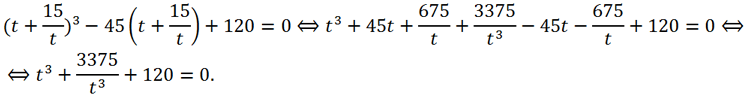
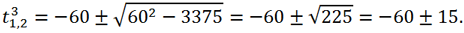
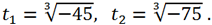 Now you can find y by the formula y = t +
Now you can find y by the formula y = t + 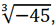 or
or 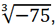 the result will be the same:
the result will be the same: