A method for solving combined equations and inequalities based on the analysis of the value regions of their left and right parts.
Let us consider a method for solving non-standard equations and inequalities, in which the ranges of two functions representing the left and right parts of the equation or inequality are compared. The essence of the method is that the range of one function has only one common point with the range of the second function. Therefore, the original equation or inequality has a solution only if the left and right sides of the equation are equal to this value.
Examples of solving combined equations and inequalities.
Example 1.
Solve the equation cos(x) = x
2 -2x + 2.
Solution.
1) The left side of the equation f
1(x) = cos(x). The range of function values E(f
1) = [-1; 1].
2) The right side of the equation f
2(x) = x
2 - 2x + 2 is a parabola with branches pointing upwards. Let's find the coordinates of the vertex:
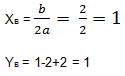
Therefore,
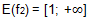
3) The solution of the equation is possible only if

But
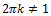
for any
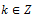
Therefore, there are no roots.
Answer: there are no roots.
Example 2.
Solve the equation
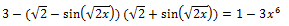 Solution.
Solution.
The range of acceptable values:
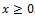
Using elementary transformations, we bring the equation to the form:
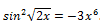
1)
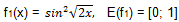
2)

3)
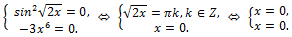 Answer:
Answer: x = 0.
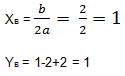
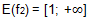 3) The solution of the equation is possible only if
3) The solution of the equation is possible only if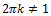 for any
for any 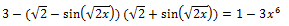 Solution.
Solution.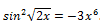 1)
1) 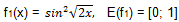 2)
2)  3)
3) 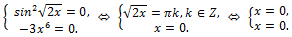 Answer: x = 0.
Answer: x = 0.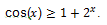 Solution.
Solution.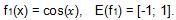 2)
2) 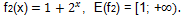 3) Therefore, the original inequality is equivalent to the system of equations
3) Therefore, the original inequality is equivalent to the system of equations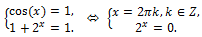 But 2x > 0 for any value of x. Therefore, the original inequality has no solution.
But 2x > 0 for any value of x. Therefore, the original inequality has no solution.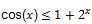 Solution.
Solution.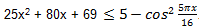 Solution.
Solution.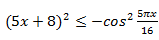 1)
1) 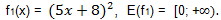 2)
2) 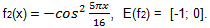 3) Therefore, the initial inequality is equivalent to a system of equations
3) Therefore, the initial inequality is equivalent to a system of equations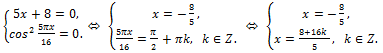 In the second equation of the system x = -8/5 at k = -1. Therefore, x = -8/5 is the solution to the original inequality.
In the second equation of the system x = -8/5 at k = -1. Therefore, x = -8/5 is the solution to the original inequality.