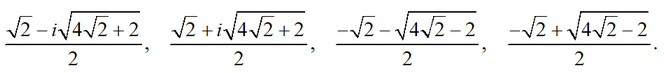The Ferrari's method for solving equations of the fourth degree

An algebraic equation of the fourth degree in the general case has the form a₀x⁴ + a₁x³ + a₂x² + a₃x + a₄ = 0,
the coefficients a_i are real (or complex) numbers, and a₀ ≠ 0. Without loss of generality, we will consider equations of degree 4 in the form x⁴ + ax³ + bx² + cx + d = 0 (since a₀ ≠ 0, we simply divide the left and right sides of the equation by a₀).
The simplest method for solving this equation was proposed by L. Ferrari. The idea of the Ferrari method is to represent the left side of the equation as the difference of the squares of two polynomials. Then this difference can be factored into two quadratic factors, and the solution of the original equation will be reduced to the solution of two quadratic equations.
We introduce an auxiliary variable t and represent the left side of the equation as

(x² + (a/2)x + t/2)² - a²x²/4 - atx/2 - t²/4 - tx² + bx² + cx + d =

 = (x² + (a/2)x + t/2)² - [(a²/4 + t - b)x² + (at/2 - c)x + t²/4 - d].

Our goal is to select a value of the auxiliary variable t such that the expression in square brackets is a perfect square. For this, it is necessary and sufficient that the discriminant of the square trinomial in square brackets is equal to zero, that is,

D = (at/2 - c)² - 4(a²/4 + t - b)(t²/4 - d) = 0.

After opening the brackets, we get the following cubic equation

t³ - bt² + (ac-4d)t - (c² + a²d - 4bd) = 0.

Let t₀ be an arbitrary root of this equation. It can be found either by Cardano's formula or by any other method. So, for t=t₀ the polynomial in square brackets is a perfect square, that is, it has one double root x₀

x₀ = -(at₀/2 - c) / (2(a²/4 + t₀ - b)).

Hence,

(a²/4 + t₀ - b)x² + (at₀/2 - c)x + t₀²/4 - d = (a²/4 + t₀ - b)(x - x₀)² = (gx + h)²

for some values of the coefficients g, h. Thus, for the initial equation it is valid

(x² + (a/2)x + t₀/2)² - (gx + h)² = 0 <=>

<=> (x² + (a/2)x + t₀/2 - gx - h)(x² + (a/2)x + t₀/2 + gx + h)<=>

<=> x² + (a/2-g)x + t₀/2 - h = 0 or x² + (a/2+g)x + t₀/2 + h = 0.

Having solved these quadratic equations, we find the 4 roots of the original equation.

Here is one useful equality. Let x₁, x₂ be the roots of the first quadratic equation, and x₃, x₄ be the roots of the second. Then by Vieta's theorem

x₁x₂ = t₀/2 - h,   x₃x₄ = t₀/2 + h.

By adding these two equalities, we obtain an expression for the auxiliary variable t, we get the expression for the auxiliary variable t₀ by the roots of the original equation:

t₀ = x₁x₂ + x₃x₄.

Let us consider examples of solving quartic equations using the Ferrari method.

Examples of solving fourth-order equations using the Ferrari method

Example 1.
Solve the equation x⁴ + 2x³ - 6x² - 5x + 2 = 0.
Solution.
For the original equation a=2, b=-6, c=-5, d=2. Let's select the perfect square on the left side of the equation

x⁴ + 2x³ - 6x² - 5x + 2 = (x² + x + t/2)² - x² - tx - t²/4 - tx² - 6x² - 5x + 2 =  (x² + x + t/2)² - [(t+7)x² + (t+5)x + t²/4 - 2].

We equate the discriminant of the expression in square brackets to zero D = (t+5)²- 4(t+7)(t²/4 - 2) = 0.
After expanding the brackets we get t³ + 6t² - 18t - 81 = 0. Integer solutions of this equation must be sought among the divisors of the free term -81: ±1, ±3,... . By direct substitution we see that t = -3 is the solution of the cubic equation. Therefore, the polynomial in square brackets at t=-3 is a perfect square

4x² + 2x + 1/4 = (2x+1/2)².

Thus, we get

x⁴ + 2x³ - 6x² - 5x + 2 = 0 <=> (x² + x - 3/2)² - (2x+1/2)² = 0.

By factoring the last equation and equating the factors to zero, we obtain two quadratic equations

x² - x - 2 = 0   or   x² + 3x - 1 = 0.

The solutions of these quadratic equations will give us 4 real roots of the original equation:

x₁ = -1, x₂ = 2, x_3,4 = (-3±√13)/2.

Answer: (-3-√13)/2, -1, (-3+√13)/2, 2.

Example 2.
Solve the equation x⁴ - 2x³ + 4x² - 2x + 3 = 0.
Solution.
For the original equation a=-2, b=4, c=-2, d=3. Let's select the perfect square on the left side of the equation

x⁴ - 2x³ + 4x² - 2x + 3 = (x² - x + t/2)² - x² + tx - t²/4 + tx² + 4x² - 2x + 3 =  (x² - x + t/2)² - [(t-3)x² + (-t+2)x + t²/4 - 3].

We equate the discriminant of the expression in square brackets to zero D = (-t+2)² - 4(t-3)(t²/4 - 3) = 0.
After expanding the brackets we get t³ - 4t² - 8t + 32 = 0. Integer solutions of this equation must be sought among the divisors of the free term 32: ±1, ±2, ±4,... . It is easy to see that t = 4 is the solution of the cubic equation. Therefore, the polynomial in square brackets at t=4 is a perfect square

x² - 2x + 1 = (x - 1)².

Thus, we get

x⁴ - 2x³ + 4x² - 2x + 3 = 0 <=> (x² - x + 2)² - (x-1)² = 0 <=> (x² - 2x + 3)(x² + 1) = 0.

By equating the factors to zero, we obtain two quadratic equations

x² - 2x + 3 = 0   or   x² + 1 = 0.

The solutions of these quadratic equations will give us the 4 complex roots of the original equation:

x_1,2 = 1±i√2,    x_3,4 = ±i.

Answer: 1-i√2, 1+i√2, -i, i.

Example 3.
Solve the equation x⁴ - 2x³ - 10x² + 24x - 24 = 0.
Solution.
For the original equation a=-2, b=-10, c=24, d=-24. Let's select the perfect square on the left side of the equation

x⁴ - 2x³ - 10x² + 24x - 24 = (x² - x + t/2)² - x² + tx - t²/4 - tx² - 10x² + 24x - 24 =  (x² - x + t/2)² - [(t+11)x² - (t+24)x + t²/4 + 24].

We equate the discriminant of the expression in square brackets to zero D = (t+24)²- 4(t+11)(t²/4 + 24) = 0.
After expanding the brackets we get t³ + 10t² + 48t + 480 = 0. It is easy to verify by a simple substitution that t> = -10 is the solution of the cubic equation. Therefore, the polynomial in square brackets at t=-10 is a perfect square

x² - 14x + 49 = (x - 7)².

Thus, we get

x⁴ - 2x³ - 10x² + 24x - 24 = 0 <=> (x² - x - 5)² - (x-7)² = 0 <=> (x² - 2x + 2)(x² - 12) = 0.

By equating the factors to zero, we obtain two quadratic equations

x² - 2x + 2 = 0   or   x² - 12 = 0.

The solutions of these quadratic equations will give us 4 roots of the original equation: 2 complex and 2 real.

x_1,2 = 1±i,    x_3,4 = ±2√3.

Answer: 1-i, 1+i, -2√3, 2√3.

Example 4.
Solve the equation x⁴ + 4x - 1 = 0.
Solution.
For the original equation a=0, b=0, c=4, d=-1. Let's select the perfect square on the left side of the equation

x⁴ + 4x - 1 = (x² + t/2)² - x²t - t²/4 + 4x - 1 =  (x² + t/2)² - [tx² - 4x + t²/4 + 1].

We equate the discriminant of the expression in square brackets to zero D = 4²- 4t(t²/4 + 1) = 0.
After expanding the brackets and dividing both parts of the equality by 4, we get t³ + 4t -16 = 0. Integer solutions of this equation must be sought among the divisors of the free term -16: ±1, ±2, ±4,... . By direct substitution we see that t = 2 is the solution of the cubic equation. Therefore, the polynomial in square brackets at t=2 is a perfect square

2x² - 4x + 2 = (√2x-√2)².

Thus, we get

x⁴ + 4x - 1 = 0 <=> (x² + 1)² - (√2x-√2)² = 0  <=> (x² - √2x + 1 + √2)(x² + √2x + 1 - √2) = 0.

By equating the factors to zero, we obtain two quadratic equations

x² - √2x + 1 + √2 = 0   or   x² + √2x + 1 - √2 = 0.

The solutions of these quadratic equations will give us 4 roots of the original equation: 2 complex and 2 real.
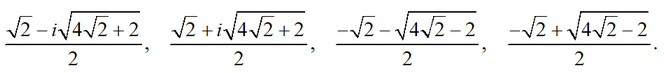
Answer: