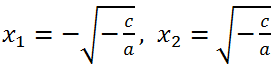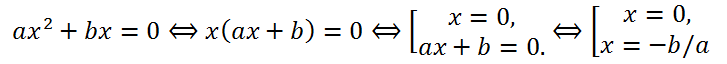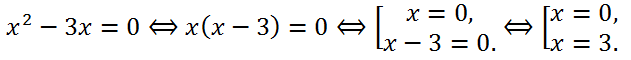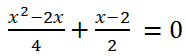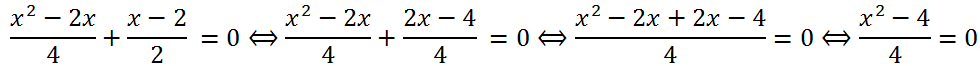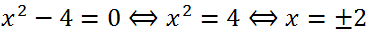The roots of an incomplete quadratic equation
1. If the quadratic equation has the form
ax2 = 0, then it has a single root x = 0.
2. If the quadratic equation has the form
ax2 + = 0, then
ax2 = - and, therefore,
.
The right side of the last equation is a number that is not equal to zero by the condition. Therefore, if the right side is less than zero, then the equation
, this means that the original equation
ax2 + = 0 has no roots.
If the right side is greater than zero, then the equation
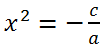
has two roots
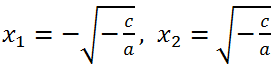
3. If the quadratic equation has the form ax
2 + bx = 0, then using the method of factorization, we get
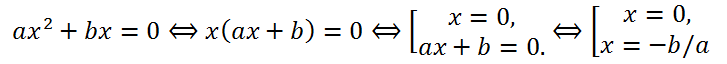
Thus, the original equation has two roots x
1=0 and x
2 = -
.
Examples of solving incomplete quadratic equations.
Example 1.Solve the quadratic equation x
2 - 3x = 0.
Solution.
The equation x
2 - 3x = 0 is an incomplete quadratic equation, so we will solve it by factoring it:
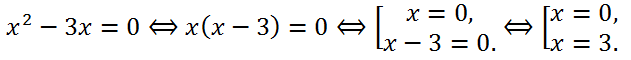 Answer: 0, 3.
Example 2.
Answer: 0, 3.
Example 2. Solve the equation
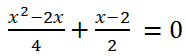 Solution.
Solution.
Let's bring the left side of the equation to a common denominator:
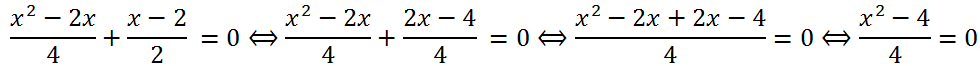
Let's multiply both parts of the equation by 4:
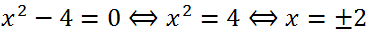 Answer:
Answer: -2, 2.
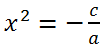 has two roots
has two roots