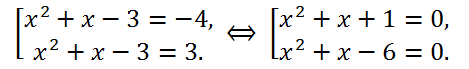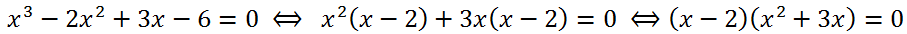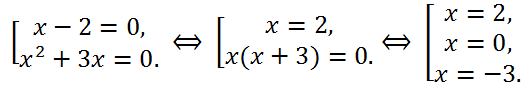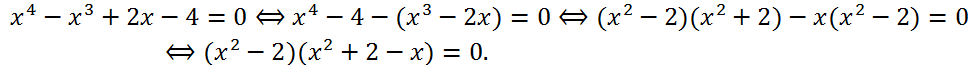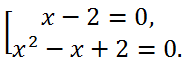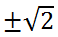General methods for solving equations

The process of solving an equation consists in a sequential transition from the original equation to a chain of equivalent equations of a simpler form than the original one. The main methods of solving equations are the method of replacing a variable and the method of factorization. Let's look at their application using examples.

Solving equations by replacing a variable

Example 1.
Solve the equation x⁸ + 15x⁴ - 16 = 0.
Solution
Let's put t = x⁴. Then the original equation will take the form t² + 15t - 16 = 0.
The roots of the resulting quadratic equation are easily found by the well-known formulas t₁ = 1, t₂ = -16.
Now for the found values t, we will find the corresponding values x.
If t = 1   <=>   x⁴ = 1   <=>   x = ±1.
If t = -16   <=>   x⁴ = -16, but this equation has no roots. So, the roots of the original equation -1, 1.
Answer: -1, 1.

Example 2.
Solve the equation (x² + x - 2)(x² + x - 3) = 12.
Solution.
Let's put x² + x - 3 = t. Then x² + x - 2 = t+1, and the initial equation takes the form
(t+1)*t = 12   <=>   t² + t - 12 = 0
Solving the resulting quadratic equation, we find its roots t₁ = -4, t₂ = 3. Thus, the original equation is equivalent to the set of equations:

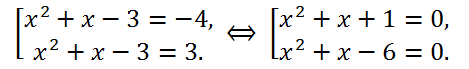
The first equation of this set has no solutions, and the roots of the second, and therefore the original, are numbers x₁ = -3, x₂ = 2.
Answer:-3, 2.

Solving equations using factorization

Example 3.
Solve the equation x³ - 2x² + 3x - 6 = 0.
Solution.

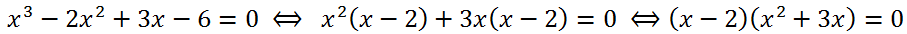
The last equation is equivalent to the set of equations:
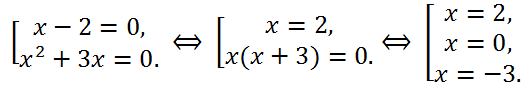
So, the roots of the original equation are numbers x₁=2, x₂=0, x₃= -3.
Answer: -3, 0, 2.

Example 4.
Solve the equation x⁴ - x³ + 2x - 4 = 0.
Solution.

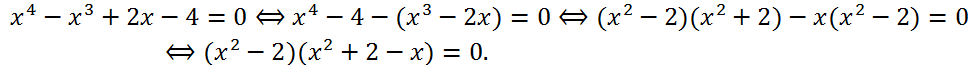
The last equation is equivalent to the set of equations:


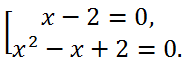
The last equation of the set has no roots, the roots of the first, and therefore the roots of the original equation
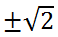Answer: -√2, √2.