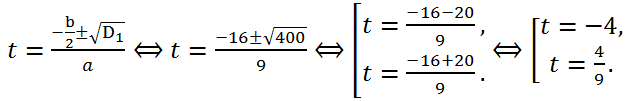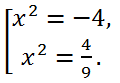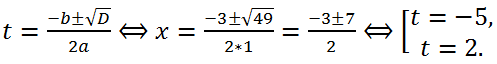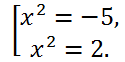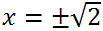Example 4.
Solve the quadratic equation x
2 + 12x + 36 = 0.
Solution.
Let's calculate the discriminant of the quadratic trinomial. We have a = 1, b = 12, c = 36.
Since b = 12 is an even number, we calculate the discriminant D
1 :
D
1 = (b/2)
2 - ac = 6
2 - 1*36 = 0, therefore, the equation has a unique root x = (-b/2)/a = (-6)/1 = -6.
This equation can be solved without calculating the discriminant by converting the quadratic trinomial using the formula of reduced multiplication:
x
2 + 12x + 36 = 0 <=> (x+6)
2 = 0 <=> x = -6.
Answer: -6.
Example 5.
Solve the quadratic equation 4x
2 -28x + 49 = 0.
Solution.
Let's calculate the discriminant of the quadratic trinomial. We have a = 4, b = -28, c = 49.
Since b = -28 - is an even number, we calculate the discriminant D
1 :
D
1 = (b/2)
2 - ac = (-14)
2 - 4*49 = 196-196 = 0, therefore, the equation has a unique root x = (-b/2)/a = 14/4 = 7/2.
This equation can also be solved without calculating the discriminant by converting the square trinomial using the reduced multiplication formula:
4x
2 -28x + 49 = 0 <=> (2x-7)
2 = 0 <=> 2x = 7 <=> x = 7/2.
Answer: 7/2.
Example 6.
Solve the equation
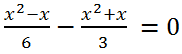 Solution.
Solution.
Let's bring the left side of the equation to a common denominator:
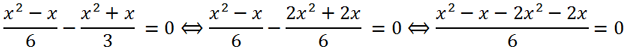
Multiplying both parts of the equation by -6, we get x
2 + 3x = 0. We will solve this incomplete quadratic equation by factoring it:
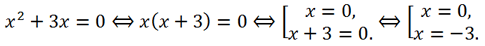 Answer:
Answer: -3, 0.
Example 7.
Solve the equation
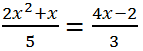 Solution.
Solution.
Let's bring the left and right sides of the equation to a common denominator:
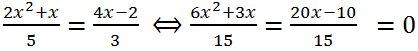
Multiplying both parts of the equation by 15, we get:
6x
2 + 3x = 20x-10 <=> 6x
2 + 3x - 20x + 10 = 0 <=> 6x
2 - 17x + 10 = 0.
Let's calculate the discriminant of the quadratic trinomial: a = 6, b = -17, c = 10.
D = b
2 - 4ac = (-17)
2 - 4*6*10 = 289 - 240 = 49 > 0, therefore, the equation has two real roots:
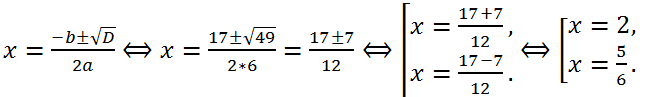 Answer:
Answer: 5/6, 2.
Example 8.
Solve the equation
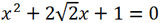 Solution.
Solution.
Let's calculate the discriminant of the quadratic trinomial: a = 1, b = 2√2, c = 1.
Since b = 2√2, that is, b is divisible by 2 (b/2 = √2), let's calculate the discriminant D
1:
D
1 = (
)
2 - ac = (√2)
2 - 1*1 = 1 > 0. Therefore, the equation has two real roots.
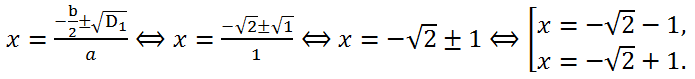 Answer:
Answer: -√2-1, -√2+1.
Example 9.
Solve the quadratic equation
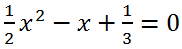 Solution.
Solution.
Multiply the left and right sides of the equation by 6:
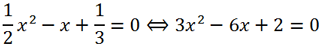
Let's calculate the discriminant of the resulting quadratic trinomial. We have a = 3, b = -6, c = 2.
Since b = -6, that is, b is divisible by 2 (b/2 = -3), let's calculate the discriminant D
1:
D
1 = (b/2)
2 - ac = 3
2 - 3*2 = 3 > 0. Therefore, the equation has two real roots.
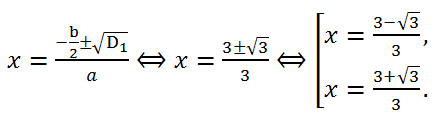 Answer:
Answer: 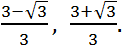 Example 10.
Example 10.
Solve the equation x
4 - 17x
2 + 16 = 0.
Solution.
The original equation is biquadratic. Replacing the variable t = x
2 => x
4 = t
2, we get an equivalent original quadratic equation:
x
4 - 17x
2 + 16 = 0 <=> t
2 - 17t + 16 = 0
Let's calculate the discriminant of a square trinomial: a = 1, b = -17, c = 16,
D = b
2 - 4ac = (-17)
2 - 4*1*16 = 289-64 = 225 > 0, therefore, the equation has two real roots:
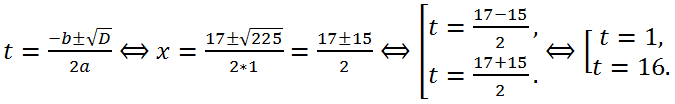
Using the found values of t, solving the equation x
2 = t, we find the roots of the original biquadratic equation:
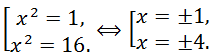
Thus, the original equation has 4 real roots.
Answer: -4, -1, 1, 4.
Example 11.
Solve the equation 9x
4 + 32x
2 - 16 = 0.
Solution.
The original equation is biquadratic. Replacing the variable t = x
2 => x
4 = t
2, we get an equivalent original quadratic equation:
9x
4 + 32x
2 - 16 = 0 <=> 9t
2 + 32t - 16 = 0
Let's calculate the discriminant of a square trinomial. We have a = 9, b = 32, c = -16.
Since b = 32, that is, b is divisible by 2 (
= 16), let's calculate the discriminant D
1:
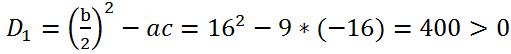
Therefore, the equation has two real roots.
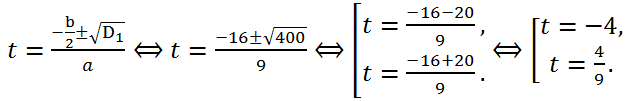
Using the found values of t, solving the equation x
2 = t, we find the roots of the original biquadratic equation:
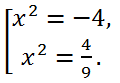
The first equation x
2 = -4 has no roots, and the second, and therefore the original, has two real roots x =
.
Answer: -2/3, 2/3.
Example 12.
Solve the equation x
4 + 3x
2 - 10 = 0.
Solution.
The original equation is biquadratic. Replacing the variable t = x
2 => x
4 = t
2, we get an equivalent original quadratic equation:
x
4 + 3x
2 - 10 = 0 <=> t
2 + 3t - 10 = 0
Let's calculate the discriminant of a square trinomial: a = 1, b = 3, c = -10,
D = b
2 - 4ac = 3
2 - 4*1*(-10) = 9+40 = 49 > 0, Therefore, the equation has two real roots:
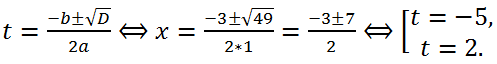
Using the found values of t, solving the equation x
2 = t, we find the roots of the original biquadratic equation:
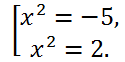
The first equation x
2 = -5 has no roots, and the second, and therefore the original, has two real roots
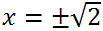 Answer:
Answer: -√2, √2.
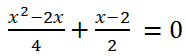 Solution.
Solution.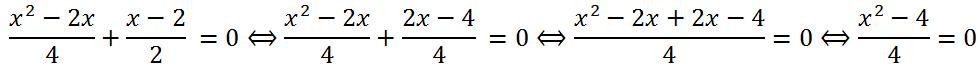
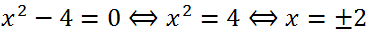
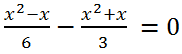
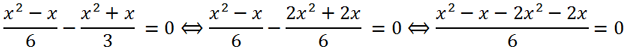 Multiplying both parts of the equation by -6, we get x2 + 3x = 0. We will solve this incomplete quadratic equation by factoring it:
Multiplying both parts of the equation by -6, we get x2 + 3x = 0. We will solve this incomplete quadratic equation by factoring it: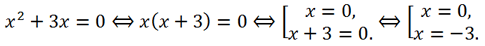 Answer: -3, 0.
Answer: -3, 0.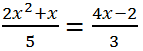 Solution.
Solution.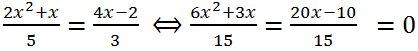
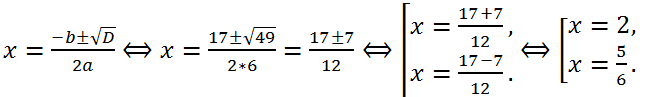
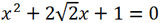
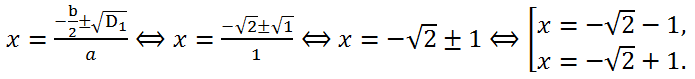
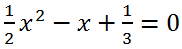
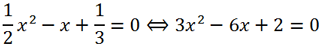
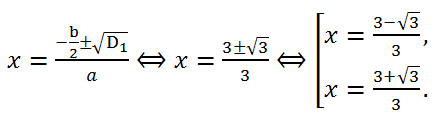
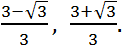
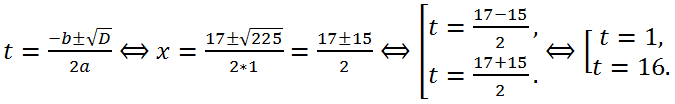
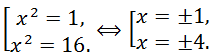
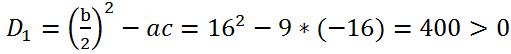 Therefore, the equation has two real roots.
Therefore, the equation has two real roots.