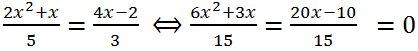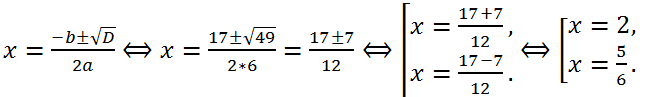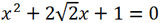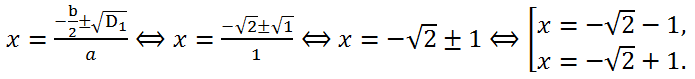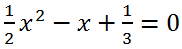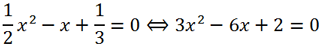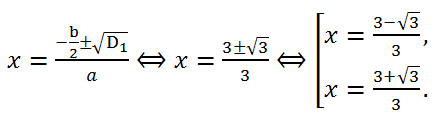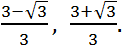Let's show how to derive these formulas:
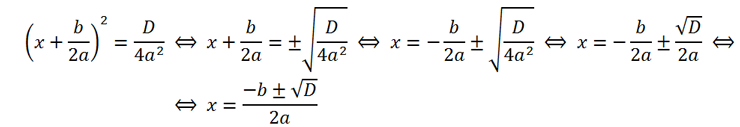
The last formula can be significantly simplified if
b is divisible by 2, that is, b = 2k. Then the formula for the roots of the quadratic equation will look like this:
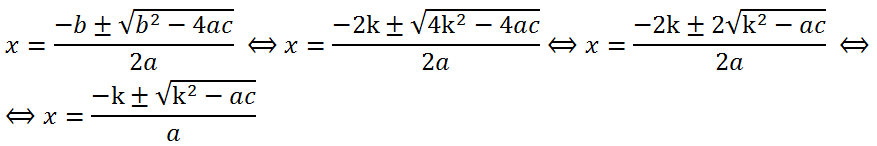
Here k = b/2.
The resulting formula for the roots of a quadratic equation in the case of an even coefficient b can be rewritten without using the letter k:
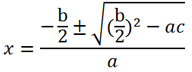
or
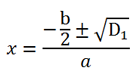
where D
1 = (
)
2 - ac.
Obviously, the obtained formulas for the roots of complete quadratic equations can also be used to solve incomplete equations, although it is easier to use methods for solving incomplete quadratic equations.
Examples of solving quadratic equations
Example 1.
Solve the quadratic equation 4x
2 -28x + 49 = 0.
Solution.
Let's calculate the discriminant of the quadratic trinomial. We have a = 4, b = -28, c = 49.
Since b = -28 - is an even number, then we calculate the discriminant D
1 :
D
1 = (
)
2 - ac = (-14)
2 - 4*49 = 196 - 196 = 0.
Therefore, the equation has a single root x = (b/2)/2 = 14/2 = 7.
This equation can also be solved without calculating the discriminant by converting the quadratic trinomial using the reduced multiplication formula:
4x
2 -28x + 49 = 0 <=> (2x - 7)
2 = 0 <=> 2x = 7 <=> x = 7/2.
Answer: 7/2.
Example 2.
Solve the equation
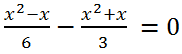 Solution.
Solution.
Let's bring the left side of the equation to a common denominator:
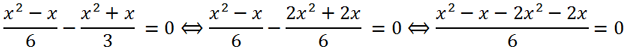
Multiplying both parts of the equation by -6, we get x
2 + 3x = 0. We will solve this incomplete quadratic equation by factoring it:
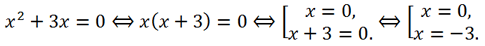 Answer:
Answer: -3, 0.
Example 3.
Solve the equation
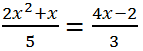 Solution.
Solution.
Let's bring the left and right sides of the equation to a common denominator:
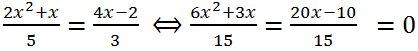
Multiplying both parts of the equation by 15, we get:
6x
2 + 3x = 20x-10 <=> 6x
2 + 3x - 20x + 10 = 0 <=> 6x
2 - 17x + 10 = 0.
Let's calculate the discriminant of the quadratic trinomial: a = 6, b = -17, c = 10.
D = b
2 - 4ac = (-17)
2 - 4*6*10 = 289 - 240 = 49 > 0, therefore, the equation has two real roots:
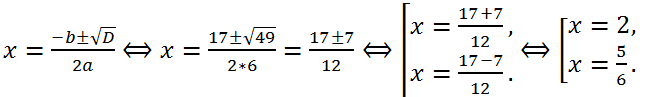 Answer:
Answer: 5/6, 2.
Example 4.
Solve the equation
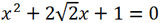 Solution.
Solution.
Let's calculate the discriminant of the quadratic trinomial. We have a = 1, b = 2√2, c = 1.
Since b = 2√2, that is, b is divisible by 2 (b/2 = √2), let's calculate the discriminant D
1:
D
1 = (
)
2 - ac = (√2)
2 - 1*1 = 1 > 0. Therefore, the equation has two real roots.
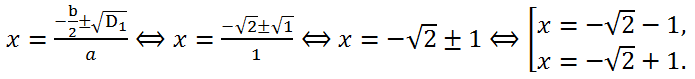 Answer:
Answer: -√2-1, -√2+1.
Example 5.
Solve the quadratic equation
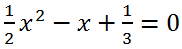 Solution.
Solution.
Multiply the left and right sides of the equation by 6:
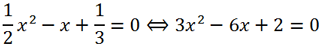
Let's calculate the discriminant of the resulting quadratic trinomial. We have a = 3, b = -6, c = 2.
Since b = -6, that is, b is divisible by 2 (b/2 = -3), let's calculate the discriminant D
1:
D
1 = (b/2)
2 - ac = 3
2 - 3*2 = 3 > 0. Therefore, the equation has two real roots.
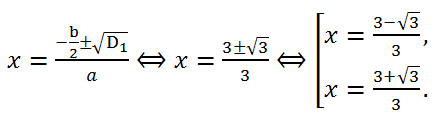 Answer:
Answer: 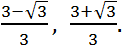
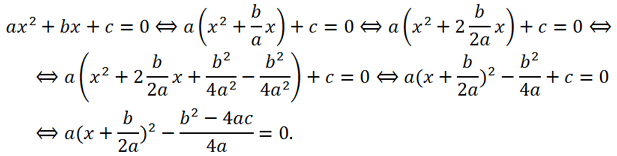
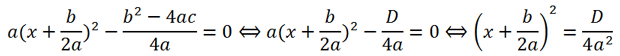
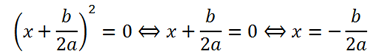
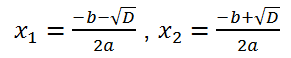
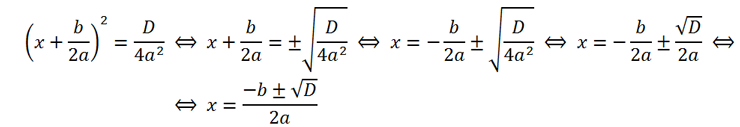
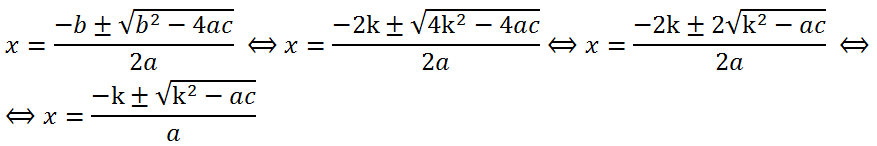 Here k = b/2.
The resulting formula for the roots of a quadratic equation in the case of an even coefficient b can be rewritten without using the letter k:
Here k = b/2.
The resulting formula for the roots of a quadratic equation in the case of an even coefficient b can be rewritten without using the letter k: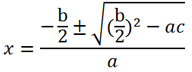 or
or
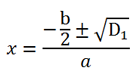 where D1 = (
where D1 = (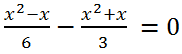 Solution.
Solution.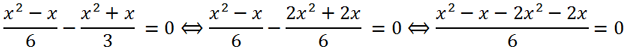
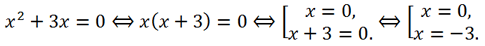 Answer: -3, 0.
Answer: -3, 0.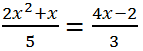 Solution.
Solution.