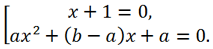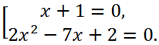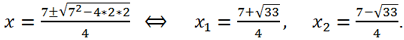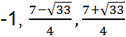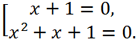Solving symmetric cubic equations

Symmetric equations of the 3 degree have the form: ax³ + bx² + bx + a = 0, a ≠ 0.
The polynomial on the left side of such equations can always be factorized as follows:
ax³ + bx² + bx + a = a(x³ + 1) + bx(x + 1) =
= a(x + 1)(x² - x + 1) + bx(x + 1) = (x + 1)(ax² + (b - a)x + a).
Therefore, the original equation is equivalent to a set of equations:


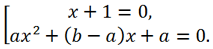
Thus, the solution of the original equation is always the number -1, and the remaining roots are the roots of the quadratic equation ax² + (b - a)x + a = 0.
Let's consider the solution of symmetric equations of degree 3 using examples.

Examples of solving symmetric cubic equations

Example 1.
Solve the equation 2x³ - 5x² - 5x + 2 = 0.
Решение.
Factorize the left side of the original equation:
2x³ - 5x² - 5x + 2 = 2(x + 1)(x² - x + 1) - 5x(x + 1) = (x + 1)(2x² - 2x + 2 - 5x) = (x + 1)(2x² - 7x + 2).
So, the original equation is equivalent to the set


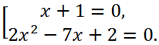
the first equation of the set has a root of -1, the second equation is solved using the formulas for the roots of a quadratic equation:

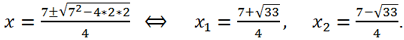Answer:
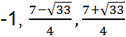Example 2.
Solve the equation x³ + 2x² + 2x + 1 = 0.
Solution.
x³ + 2x² + 2x + 1 = (x + 1)(x² - x + 1) + 2x(x + 1) = (x + 1)(x² - x + 1 + 2x) = (x + 1)(x² + x + 1). So, the original equation is equivalent to the set


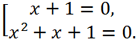
The first equation of the set has a root of -1, the second equation has no roots, since the discriminant D = 1 - 4 = -3  <  0.
Answer: -1.