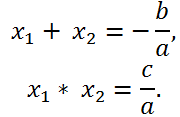Vieta's theorem for solving quadratic equations

Vieta's theorem establishes a connection between the coefficients of a quadratic equation and its roots, if they exist.
THE THEOREM. If x₁, x₂ are the roots of the quadratic equation ax² + bx + c = 0, then the sum of the roots is

-

b/a

, and the product of the roots is equal to

c/a

:
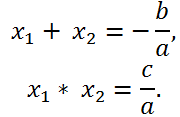
For the reduced quadratic equation x² + px + q = 0 Vieta's theorem can be formulated quite simply: the sum of the roots of the reduced quadratic equation is equal to the coefficient at x, taken with the inverse sign, and the product of the roots is equal to the free term:
x₁ + x₂ = - p,
x₁ * x₂ = q.

The proof of this theorem follows directly from the formulas for the roots of the quadratic equation.
The inverse theorem is also true. If the numbers x₁, x₂ are such that
x₁ + x₂ = - p,
x₁ * x₂ = q.
then these numbers are the roots of the quadratic equation x² + px + q = 0.

With this theorem, many quadratic equations can be easily solved without using cumbersome formulas for its roots. In addition, very often one of the roots of the equation is the number x₁ = 1 or x₁ = -1, which is easily verified by a simple substitution. Then the second root can be quickly found from the equality x₁* x₂ = , so x₂ =  or x₂ = -. Vieta's theorem can also be used to verify the found roots of a quadratic equation. Let's consider the application of this theorem using examples.

Examples of solving quadratic equations using Vieta's theorem

Example 1.
Solve the equation x² + 5x + 6 = 0.
Solution.
By the converse of Vieta's theorem
x₁ + x₂ = - 5,
x₁ * x₂ = 6.
The number 6 = 2*3 = 1*6, therefore, it is easy to find a solution to this system x₁ = -2, x₂ = -3.
Answer: -3, -2.

Example 2.
Solve the equation x² - 12x + 11 = 0.
Solution.
Obviously, x₁ = 1 is the root of the quadratic equation. But x₁* x₂ = 11, so the second root is 11.
Answer: 1, 11.

Example 3.
Solve the equation 2013x² - 2012x - 1 = 0.
Solution.
Obviously, x₁ = 1 is the root of the quadratic equation. We verify this by direct substitution into the original equation. But x₁* x₂ = , so the second root is equal to . Solving the original equation using the formulas for finding the roots of a quadratic equation would be much more difficult from a computational point of view.
Answer: -1/2013, 1.

Example 4.
Solve the equation 5699x² + 5691x - 8 = 0.
Solution.
Obviously, x₁ = -1 is the root of the quadratic equation. We verify this by direct substitution into the original equation. But x₁* x₂ = , значит, второй корень равен .
Answer: -1, 8/5699.