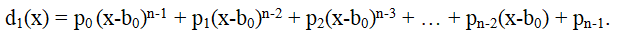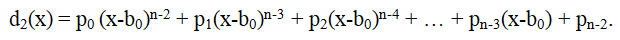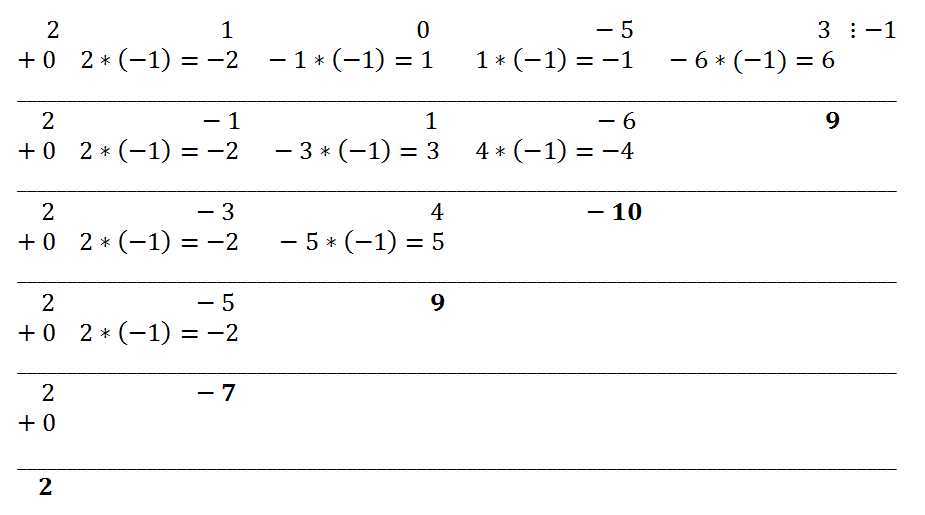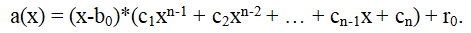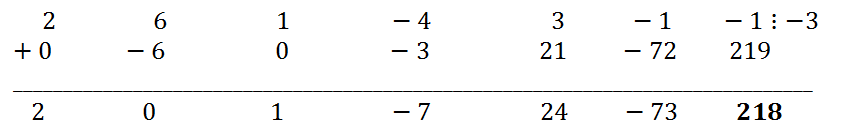Example 1.
Divide the polynomial x
4 - 3x
3 - 3x
2 + 7x + 6 by the binomial x-3 using Horner's scheme.
Solution.
The dividend a(x)=x
4 - 3x
3 - 3x
2 + 7x + 6, b
0=3. In accordance with Horner's scheme, we fill in the table
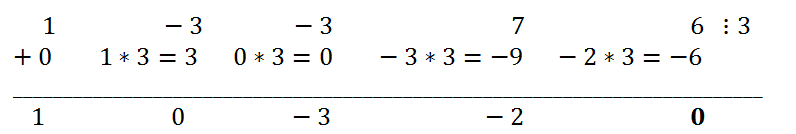
Thus, the remainder r (the last number in the third row) is zero. This means that the polynomial x
4 - 3x
3 - 3x
2 + 7x + 6 is completely divisible by x - 3. Quotient (x)=1*x
3 + 0*x
2 - 3x - 2.
Answer: x
4 - 3x
3 - 3x
2 + 7x + 6=(x
3 - 3x - 2)*(x - 3).
Example 2.
Divide the polynomial 2x
5 + 5x
4 - 4x
3 + 612 by the binomial x + 4 using Horner's scheme.
Solution.
The dividend a(x)= 2x
5 + 5x
4 - 4x
3 + 612, b
0=-4. In accordance with Horner's scheme, we fill in the table
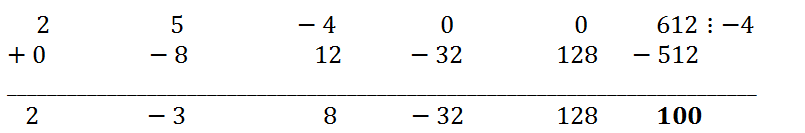
The remainder r = 100 - this is the last number in the third row. The quotient (x)=2*x
4 - 3*x
3 - 8*x
2 - 32*x + 128.
Answer: 2x
5 + 5x
4 - 4x
3 + 612 = (2x
4 - 3x
3 - 8x
2 - 32x + 128)*(x + 4) + 100.
The division of a polynomial a(x) by a binomial of the form b
1x - b
0 is easily reduced to the case of division by x - b
0.
Let a(x) = (b
1x - b
0)*c(x) + r
0, we transform this expression as follows:
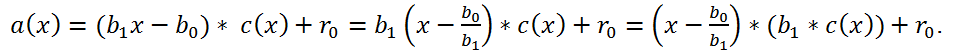
An analysis of the last expression shows that the remainder of a(x) divided by b
1x - b
0 is the same as the remainder of a(x) divided by x - b
0/b
1, and the coefficients of the quotient c(x) are obtained from the coefficients of the quotient from division by x - b
0/b
1 by dividing them by b
1.
Example 3.
Divide the polynomial x
3 - 6x
2 + 5x + 2 by the binomial 2x + 1 using Horner's scheme.
Solution.
Since 2x + 1=2(x + 1/2), using Horner's scheme we will divide the original polynomial by x+1/2, then divide the resulting coefficients of the quotient by 2.
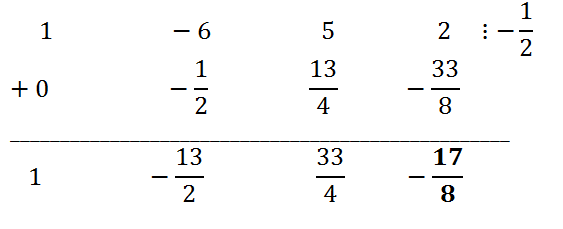
The remainder r
0 = -17/8. The coefficients of the quotient are obtained by dividing the coefficients in the third row of the table by 2. Thus, the quotient of dividing the original polynomial by 2x + 1
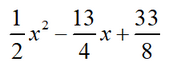 Answer:
Answer:
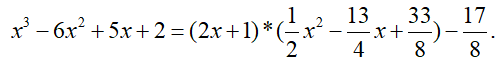 Example 4.
Example 4.
Divide the polynomial x
5 - x
3 + 2x - 1 by the binomial 3 - 2x using Horner's scheme.
Solution.
Since 3 - 2x = - 2(x - 3/2), using Horner's scheme we will divide the original polynomial by x - 3/2, then we divide the obtained quotient coefficients by -2.
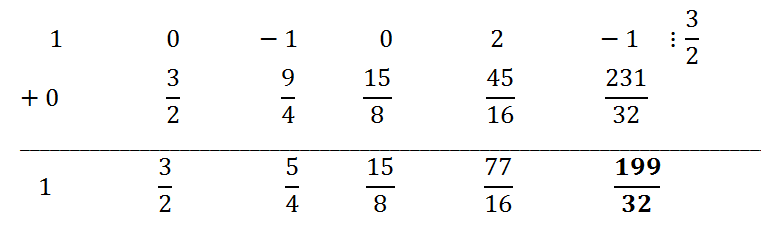
The remainder r
0 = 199/32. The coefficients of the quotient are obtained by dividing the coefficients in the third row of the table by -2. Thus, the quotient of dividing the original polynomial by 3 - 2x
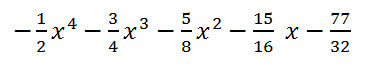 Answer:
Answer:
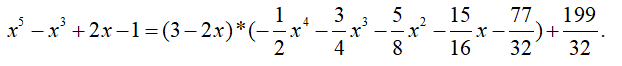
Using the Horner's scheme to decompose a polynomial by powers of a binomial
Let us consider another application of Horner's scheme – decomposition of a polynomial by powers of a binomial. For any polynomial
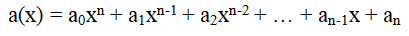
where a
0 ≠ 0, n ≥ 1,
and for any number b
0 we can write the decomposition of a(x) by powers x - b
0:
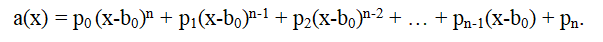
As can be seen from this formula, in order to calculate p
n, it is necessary to divide the polynomial a(x) by x - b
0 and find the remainder r = p
n. In the quotient, we get the polynomial
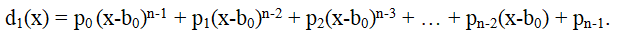
Now, to calculate p
n-1, you need to divide the polynomial d
1 (x) by x - b
0 and find the remainder r=p
n-1. In the quotient we get the polynomial
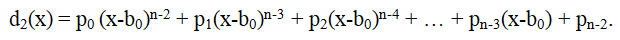
Then we continue dividing until the quotient is a number. The remainder obtained in the last step will be equal to p
1, and the quotient d
n=p
0.
At each step, division by x-b
0 will be carried out using Horner's scheme. It is very convenient to write down the calculation results in one common table. Let's consider the corresponding example.
Example 5.
Decompose the polynomial 2x
4 + x
3 - 5x + 3 by the powers of the binomial x + 1.
Solution.
We will perform all calculations by sequentially filling in the table according to the algorithm.
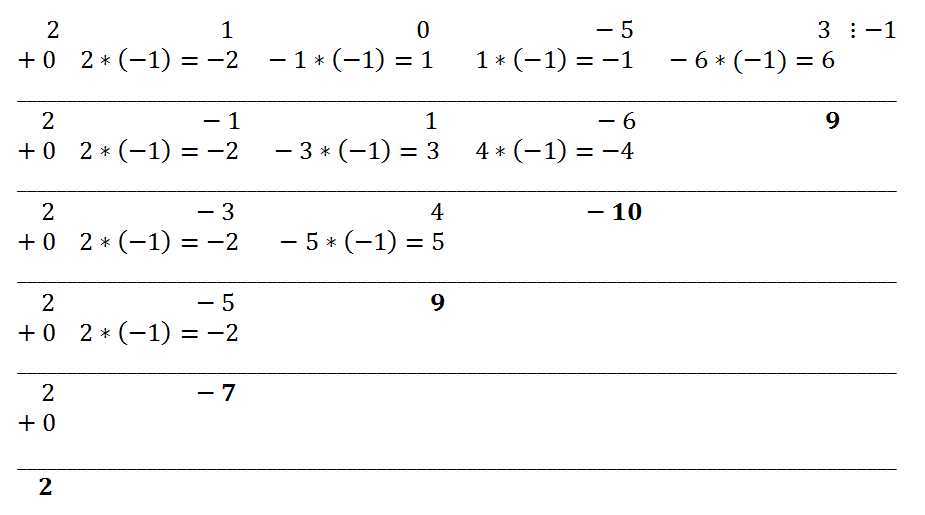
Thus, we obtain that the remainder of the division of the original polynomial by x+1 is 9, the coefficients of the quotient are 2,-7,9,-10.
Answer:
2x
4 + x
3 - 5x + 3 = 2(x + 1)
4 - 7(x + 1)
3 + 9(x + 1)
2 - 10(x + 1) + 9.
Calculating the value of a polynomial at a given point using Horner's scheme
Another problem that can be solved using Horner's scheme is calculating the value of a polynomial at a given point. Let the polynomial a(x) be divisible by the binomial x-b
0 with remainder r
0. That is
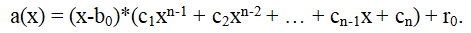
If we substitute the value x=b
0 into this equality, we get a(b
0)=r
0. Thus, we have proved Bezout's theorem.
Bezout's theorem. If x
0 is an arbitrary number, then dividing the polynomial a(x) by the binomial x-x
0 results in a remainder equal to the value of the polynomial for x=x
0, that is r
0= a(x
0).
Thus, using Horner's scheme, one can find the value of a polynomial for a given value x=x
0 as the remainder of dividing this polynomial by the binomial x-x
0. Sometimes this is much easier to do than substituting x
0 into the original polynomial.
Bezout's theorem has a very important consequence.
Consequence. A number x
0 is a root of a polynomial a(x) if and only if the polynomial a(x) is divisible by the binomial x-x
0.
This consequenc allows us to check whether a number x
0 is a root of a polynomial by calculating the remainder of the division of the polynomial by the binomial x-x
0.
Example 6.
Calculate the value of a polynomial 2x
6 + 6x
5 + x
4 - 4x
3 + 3x
2 - x - 1 at x=-3.
Solution.
Calculating the value of a polynomial at x=-3 is equivalent to finding the remainder when dividing this polynomial by x+3. To do this, we will use Horner's scheme
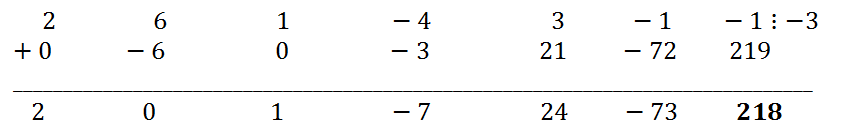
The remainder r (this is the last number in the third line) is 218.
The quotient (x)=2x
5 + x
3 - 7x
2 + 24x - 73.
2x
6 + 6x
5 + x
4 - 4x
3 + 3x
2 - x - 1=(2x
5 + x
3 - 7x
2 + 24x - 73)*(x+3)+218.
Answer: 218.
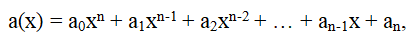 by the binomial b(x) = x - b0, b(x)=x-b0, that is, it is required to represent the polynomial a(x) in the form
by the binomial b(x) = x - b0, b(x)=x-b0, that is, it is required to represent the polynomial a(x) in the form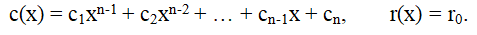 That is
That is
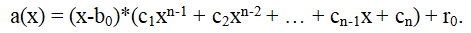 We multiply x-b0 and c(x), add it to r0 and equate the coefficients of the polynomials with the same powers of x on the left and right sides of the equality:
We multiply x-b0 and c(x), add it to r0 and equate the coefficients of the polynomials with the same powers of x on the left and right sides of the equality: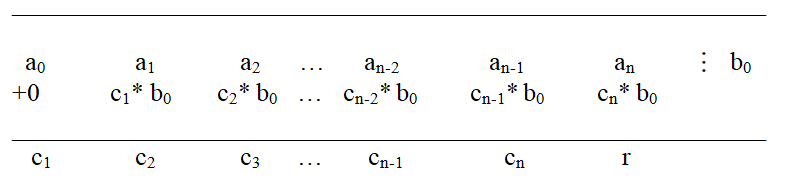
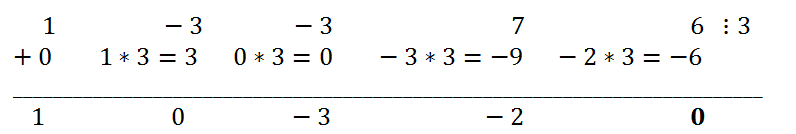
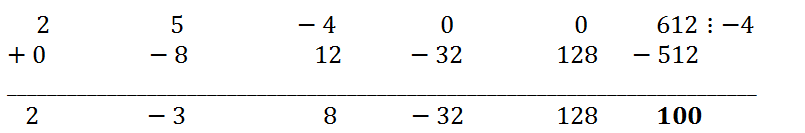
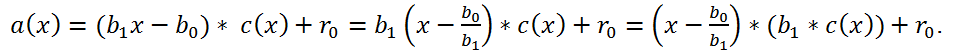
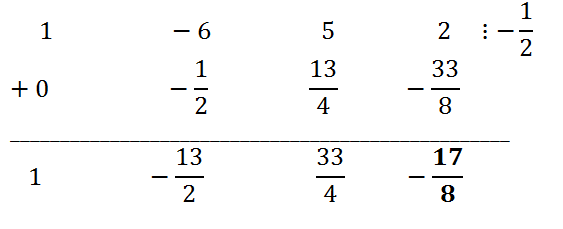
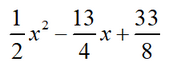
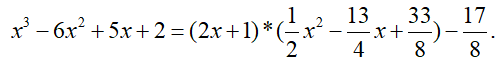
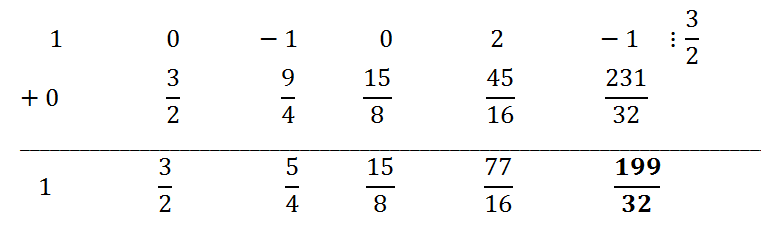
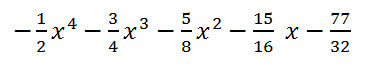
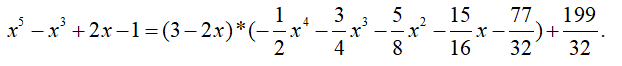
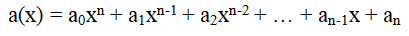 where a0 ≠ 0, n ≥ 1,
and for any number b0 we can write the decomposition of a(x) by powers x - b0:
where a0 ≠ 0, n ≥ 1,
and for any number b0 we can write the decomposition of a(x) by powers x - b0: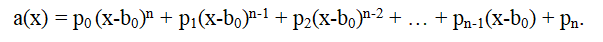 As can be seen from this formula, in order to calculate pn, it is necessary to divide the polynomial a(x) by x - b0 and find the remainder r = pn. In the quotient, we get the polynomial
As can be seen from this formula, in order to calculate pn, it is necessary to divide the polynomial a(x) by x - b0 and find the remainder r = pn. In the quotient, we get the polynomial