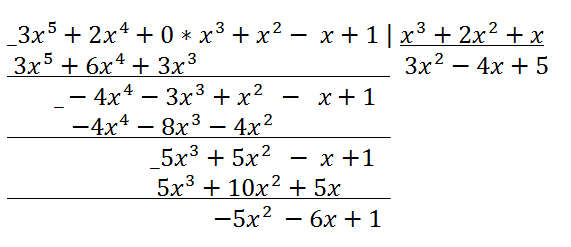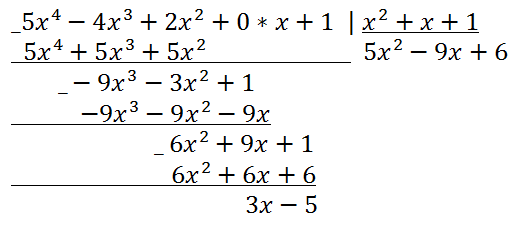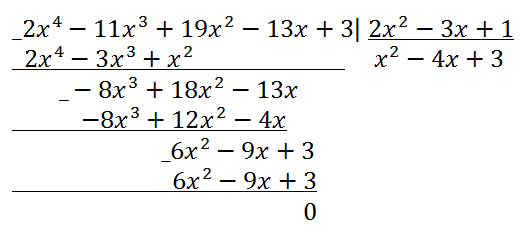Dividing a polynomial by a polynomial

An expression of the form

P(x)=a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n

is called a polynomial in x of degree n with real coefficients , if the coefficients a_i are real numbers and a₀ ≠ 0. The coefficient a_n is called the free term of the polynomial.


If P(x), b(x), c(x) – are polynomials such that P(x)=b(x) * c(x), then the polynomial P(x) is said to be completely divisible by the polynomial b(x) or by the polynomial c(x).

If P(x)=b(x)*c(x) + r(x) and the degree of r(x) is less than the degree of the polynomial b(x), then the polynomial P(x) is said to be divisible by the polynomial b(x) with remainder r(x). Here, the polynomial P(x) is the dividend, the polynomial b(x) is the divisor, the polynomial c(x) is the quotient, and the polynomial r(x) is the remainder.

When dividing (with or without remainder) a polynomial by a polynomial in the quotient, a polynomial is obtained whose degree is equal to the difference between the degrees of the divisor and the divisor.

The simplest way to divide polynomials is by dividing by a column or a "corner", similar to the division of natural numbers.

Dividing a polynomial by a polynomial by a column (angle)

The algorithm of dividing a polynomial by a polynomial by a column:

1. We write down both polynomials in descending order of degrees.

2. The highest term of the dividend is divided by the highest term of the divisor. The resulting monomial is another member of the quotient.

3. We subtract from the dividend the product of the first term of the quotient by the divisor. The resulting polynomial is a remainder.

4. If the degree of the remainder is greater than or equal to the degree of the divisor, then we use this remainder as a divisor and proceed to step 2 to obtain the next quotient term.

If the degree of the remainder is less than the degree of the divisor, then the division process is completed, and the last remainder will be the remainder of the division of the original polynomials.

If the remainder is zero, then the polynomials are completely divided, without any remainder.

Let's consider the operation of the algorithm for dividing polynomials by a column using examples.

Dividing a polynomial by a polynomial with a remainder

Example 1.
Divide the polynomial 3x⁵ + 2x⁴ + x² - x + 1 by the polynomial x³ + 2x² + x.
Answer.
Let's describe the algorithm for dividing polynomials for this example in steps.

1. Let's write down both polynomials in descending order of degrees
3x⁵ + 2x⁴ + x² - x + 1 = 3x⁵ + 2x⁴ + 0*x³ + x² - x + 1,
x³ + 2x² + x = x³ + 2x² + x

2. We divide 3x⁵ by the first term of the dividend x³. We get the first member of the quotient 3x².

3. We multiply the first term of the quotient 3x² by the divisor x³ + 2x² + x. We get a polynomial 3x⁵ + 6x⁴ + 3x³ and write it under the dividend.

4. We subtract from the dividend 3x⁵ + 2x⁴ + 0*x³ + x² - x + 1 the polynomial written under it. We get the first remainder -4x⁴ - 3x³ + x² - x + 1.

5. We divide the first term of the first remainder -4x⁴ by the first term of the divisor x³. We get the second term of the quotient -4x.

6. We multiply the second term of the quotient -4x by the divisor x³+2x²+x. We get the polynomial -4x⁴ - 8x³ - 4x² and write it under the first remainder.

7. We subtract from the first remainder -4x⁴ - 3x³ + x² - x + 1 the polynomial written under it. We get the second remainder 5x³ + 5x² - x + 1.

8. We divide the first term of the second remainder 5x³ by the first term of the divisor x³. We get the third term of the quotient 5.

9. We multiply the third term of the quotient 5 by the divisor x³ + 2x² + x. We get the polynomial 5x³ + 10x² + 5x and write it under the second remainder.

10. We subtract from the second remainder 5x³ + 5x² - x + 1 the polynomial written under it. We get the third remainder -5x² - 6x + 1.

11. The degree of the third remainder is less than the degree of the divisor, therefore the division process is complete. The quotient of division 3x² - 4x + 5, the remainder -5x² - 6x + 1.

Let's write the division of polynomials as a "corner" division.



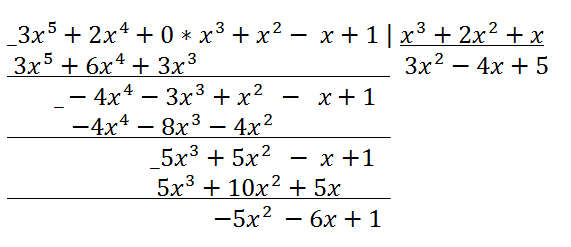Answer: 3x⁵ + 2x⁴ + x² - x + 1 = (3x² - 4x + 5)*(x³ + 2x² + x) - 5x² - 6x + 1.

Example 2.
Divide the polynomial 5x⁴ - 4x³ + 2x² + 1 by the polynomial x² + x + 1.
Solution.
Dividing a polynomial by a polynomial by a column (corner)



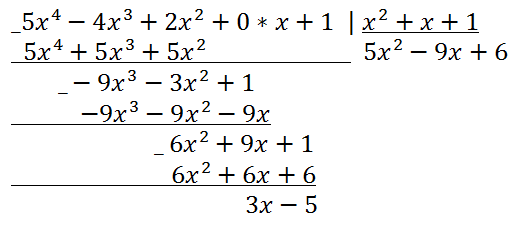Answer: 5x⁴ - 4x³ + 2x² + 1 = (5x² - 9x + 6)*(x² + x + 1) + 3x - 5.

Dividing a polynomial by a polynomial without remainder

Example 3.
Divide the polynomial 2x⁴ - 11x³ + 19x² - 13x + 3 by the polynomial 2x² - 3x + 1.
Solution.
Dividing a polynomial by a polynomial by a column (corner)


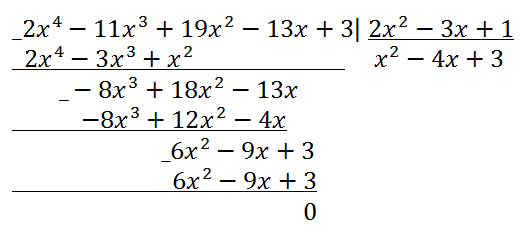
The polynomial 2x⁴-11x³+19x²-13x+3 is the dividend by the polynomial 2x² - 3x + 1 with no remainder.

Answer: 2x⁴ - 11x³ + 19x² - 13x + 3 = (x² - 4x + 3)*(2x² - 3x + 1).