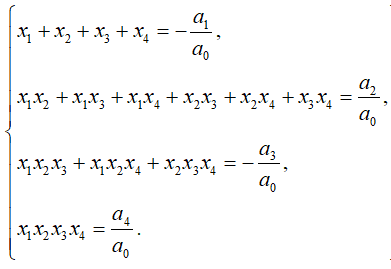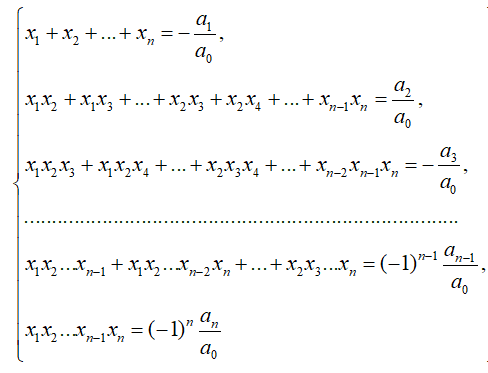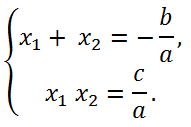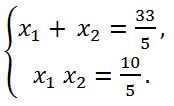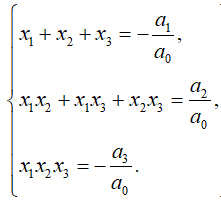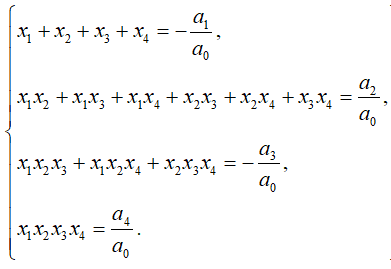Generalized Vieta's theorem

If the numbers x₁, x₂,...,x_n are the roots of a polynomial of the nth degree (n is equal to the number of roots taking into account their multiplicity)

a₀*xⁿ + a₁*x^n-1 + a₂*x^n-2 + ... + a_n-1*x + a_n, a₀ ≠0,

then the following equalities are true:


These equalities are called Vieta's formulas.
Let us write them out separately for the roots of polynomials of the second, third and fourth orders.

Vieta's formulas for the roots of a square trinomial

For the roots of the square trinomial ax² + bx + c the following equalities are true:


Vieta's formulas for the roots of a square trinomial allow one to select its integer roots (if they exist) without solving the quadratic equation.

Example 1.
Factorize a square trinomial x² - 2012x + 2011.
Solution.
It is easy to see that x = 1 is a root of the trinomial. We verify this by a simple substitution. According to Vieta's formula

x₁x₂ =  = 2011 <=> 1*x₂ = 2011 <=> x₂ = 2011. Hence, x² - 2012x + 2011 = (x - 1)(x - 2011).

Answer: x² - 2012x + 2011 = (x - 1)(x - 2011).

Example 2.
Factorize a square trinomial 2012x² + 2011x - 1.
Solution.
A simple substitution easily verifies that x = -1 is a root of a square trinomial. According to Vieta's formula

x₁x₂ =  <=> -1*x₂ =  <=> x₂ = .

Hence, 2012x² + 2011x - 1= 2012(x + 1)(x - ) = (x+1)(2012x-1).
Answer: 2012x² + 2011x - 1= 2012(x + 1)(x - ) = (x+1)(2012x-1).

Thus, very often Vieta's formulas allow one to quickly select the whole roots of a square trinomial without performing cumbersome calculations. In addition, one can draw conclusions about the signs of the roots of the equation based on the coefficients of the trinomial. For example, if the roots of the trinomial exist, and > 0, then either both roots are positive or both are negative.

Example 3.
Determine the signs of the roots of a quadratic equation 5x² - 33x + 10 = 0 without solving it.
Solution.
Discriminant of the equation D = b² - 4ac = 33² - 4*5*10 > 0, therefore, the equation has two real roots. According to Vieta's formulas


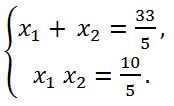
That is x₁x₂ > 0, then both roots have the same sign. But the sum of the roots > 0, therefore both roots are positive numbers.
Answer: the equation has two positive roots.

In addition, Vieta's formulas allow you to quickly check whether a given set of numbers are the roots of a polynomial. In general, Vieta's formulas are a very useful tool in solving a wide variety of problems with polynomials.

Let us write out Vieta's formulas for polynomials of the third and fourth orders.

Vieta's formulas for the roots of a third-order polynomial

If x₁, x₂, x₃ - roots of a polynomial a₀*x³ + a₁*x² + a₂*x + a₃, then the following equalities are true for them:

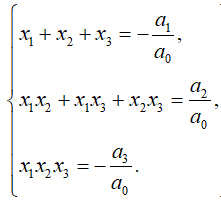
Vieta's formulas for the roots of a fourth-order polynomial

If x₁, x₂, x₃, x₄ - roots of a polynomial a₀*x⁴ + a₁*x³ + a₂*x² + a₃*x + a₄, then the following equalities are valid for them: