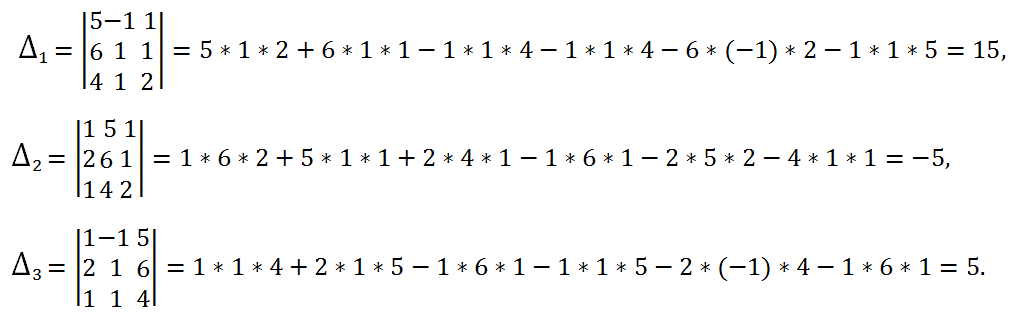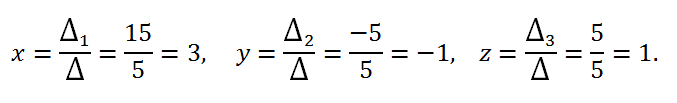Since the calculation of determinants of the 4th and higher orders is a rather cumbersome procedure, finding the roots of a system of linear equations using Cramer's formulas is appropriate for systems of two or three equations. Let us write out formulas for calculating determinants of the second and third orders.
The determinant of the second order
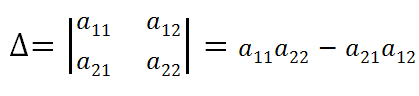
The determinant of the third order
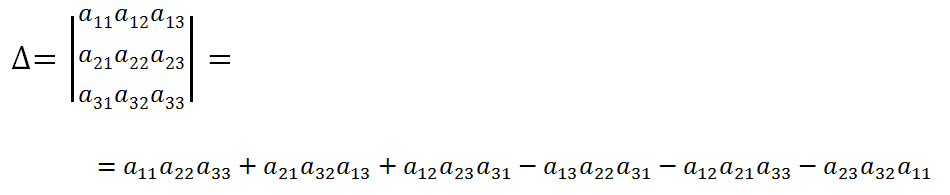
Let's consider the application of Cramer's formulas using examples.
Examples of solving systems of linear equations using Cramer's formulas
Example 1.
Solve a system of two linear equations with two unknowns
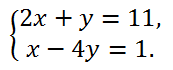 Solution.
Solution.
1) Let's calculate the determinant of this system:
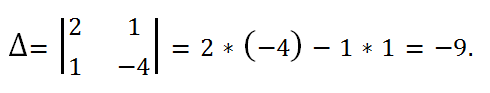
The determinant of the system is equal to -9 ≠ 0, therefore, the system is compatible and has a unique solution.
2) Let's calculate two determinants that are obtained from the determinant of the system by replacing the first and second columns, respectively, with a column of free terms:
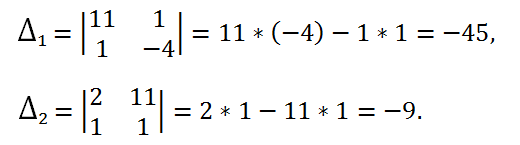
3) Using Cramer's formulas we calculate the values of the unknowns:
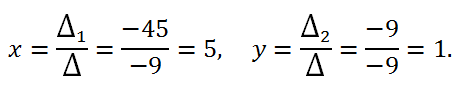 Answer:
Answer: x = 5, y = 1.
Example 2.
Solve a system of three linear equations with three unknowns
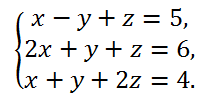 Solution.
Solution.
1) Let's calculate the determinant of this system:
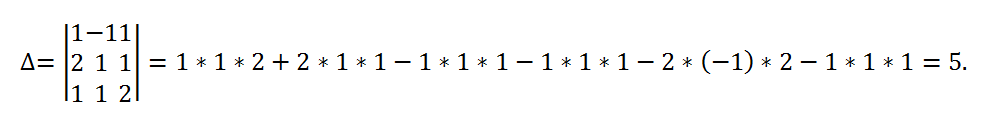
The determinant of the system is equal to 5 ≠ 0, therefore, the system is compatible and has a unique solution.
2) Let's calculate 3 determinants, which are obtained from the determinant of the system by replacing the first, second and third columns, respectively, with a column of free terms:
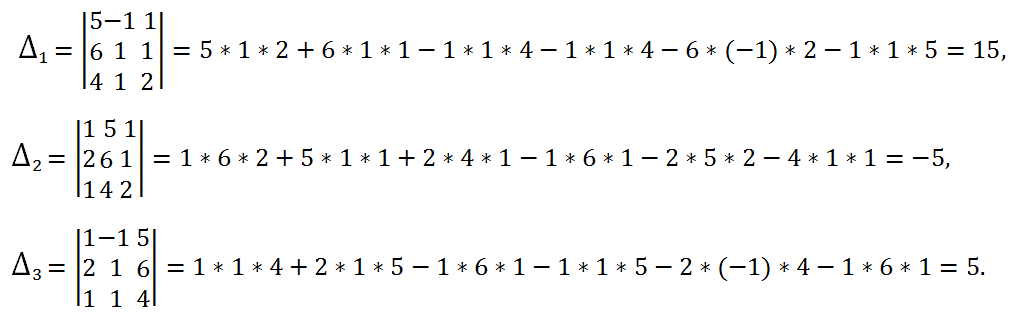
3) Using Cramer's formulas we calculate the values of the unknowns:
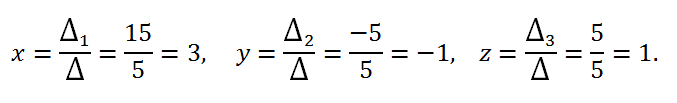 Answer:
Answer: x = 3, y = -1, z = 1.
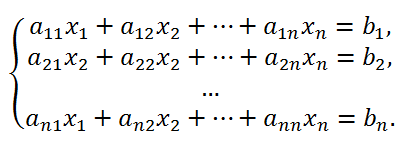
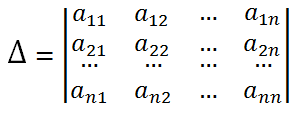

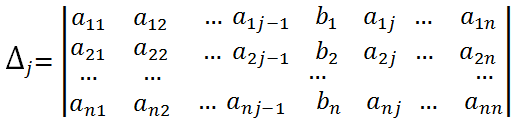
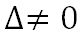
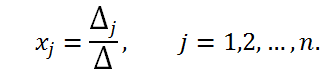
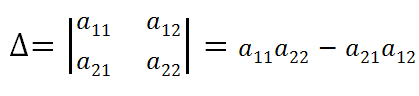
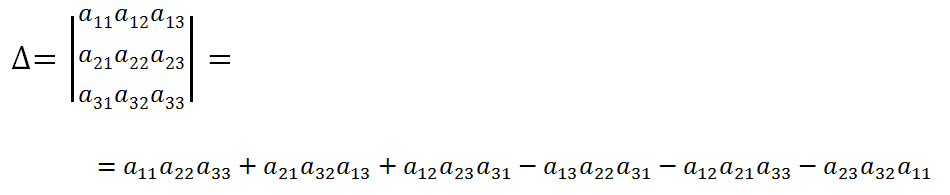
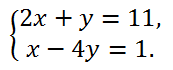 Solution.
Solution.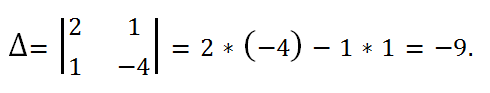 The determinant of the system is equal to -9 ≠ 0, therefore, the system is compatible and has a unique solution.
The determinant of the system is equal to -9 ≠ 0, therefore, the system is compatible and has a unique solution.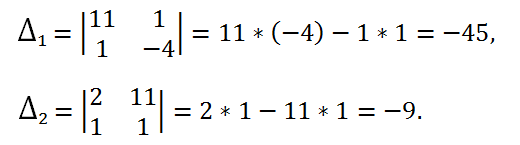
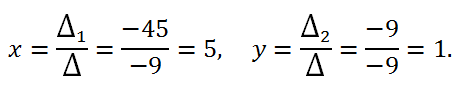
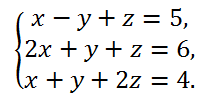 Solution.
Solution.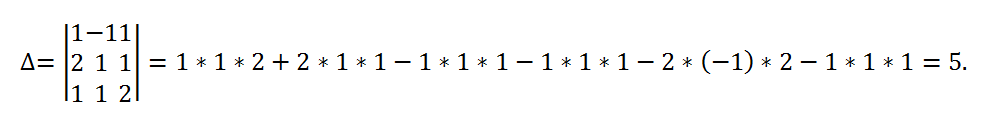 The determinant of the system is equal to 5 ≠ 0, therefore, the system is compatible and has a unique solution.
The determinant of the system is equal to 5 ≠ 0, therefore, the system is compatible and has a unique solution.