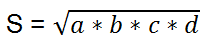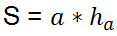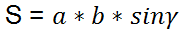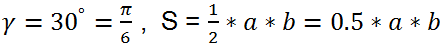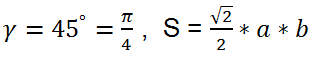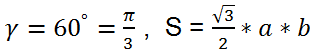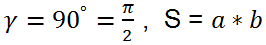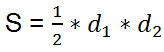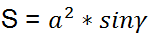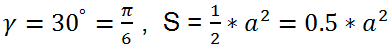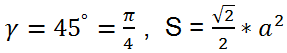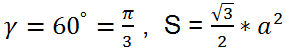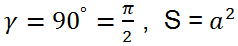Formulas for the area of a convex quadrilateral
Designations:
a,
b,
c and
d – sides of the quadrilateral;
r - radius of the
inscribed circle,
R - radius of the
circumscribed circle;
ha –
height dropped to the side
a;
p – semiperimeter,
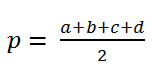 d1
d1,
d2 - diagonals of a quadrilateral.
Area of an arbitrary convex quadrilateral
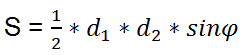
where
φ - the angle between diagonals.
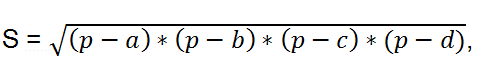
where
p - the semiperimeter.
S = p * r
If a circle can be inscribed in a quadrilateral (a circle can be inscribed in a quadrilateral when the sums of its opposite sides are equal), and a circle can be circumscribed around it (a quadrilateral can be inscribed in a circle if the sum of its opposite angles is equal to 180°), then its area is equal to:
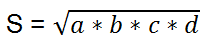
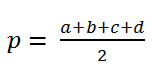
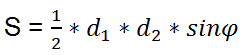 where φ - the angle between diagonals.
where φ - the angle between diagonals.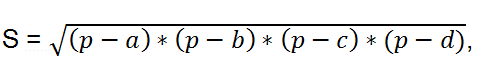 where p - the semiperimeter.
where p - the semiperimeter.