Central angle, inscribed angle
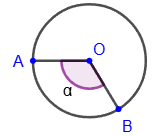
Central angle is the angle formed by two radii: ∠AOB.
The degree measure of an arc of a circle is called the degree measure of the corresponding central angle: ∪AB = ∠AOB.
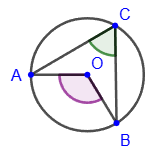
An inscribed angle is an angle formed by two chords originating from the same point on a circle: ∠ACB.
The inscribed angle is equal to half of the corresponding central angle (in other words, half the magnitude of the arc on which it rests): ∠AСB = ½∠AOB = ½∪AB.
Properties of angles and arcs:
1) Inscribed angles resting on the same arc or on equal arcs are equal.
2) An inscribed angle is a right angle if and only if it rests on a diameter.
3) Equal arcs are subtended by equal chords.
4) Equal chords subtend equal arcs.
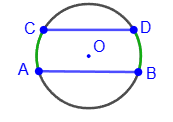
5) The arcs of the circle enclosed between the parallel chords are equal: ∪AC = ∪BD.