Definitions: circle, chord, tangent, internal and external tangency of circles, secant

Circle

A circle is a geometrical locus of points equidistant from one point - the center of the circle. The radius of a circle is the distance from the center of the circle to any point on the circle. The radius is also called any segment connecting a point of the circle to its center.
A chord of a circle is a segment connecting any two points on the circle. A diameter of a circle is a chord passing through the center of the circle.
In the figure, point O is the center of the circle, segment OA (or OB) is the radius of the circle, segment AB is the diameter of the circle, segment CD is the chord.

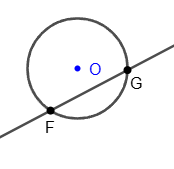
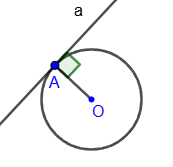
Tangent to a circle

A tangent is a line that passes through a point on a circle perpendicular to the radius drawn to that point.
A tangent to a circle has no other common points with it except the point of tangency.
In the figure, the line a, perpendicular to the radius AO, is a tangent. Point A is the point of tangency.

Internal tangency of circles

Two circles are tangent to each other if they have a common tangent at a point belonging to both circles.
The tangency of circles is called internal if the centers of the circles lie on the same side of their common tangent.
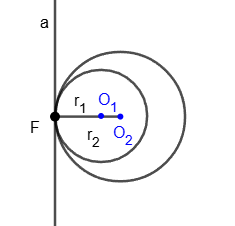
The formula for the distance between the centers of the circles is: O₁O₂ = r₂ - r₁.

External tangency of circles

The tangency of circles is called external if the centers of the circles lie on different sides of their common tangent.
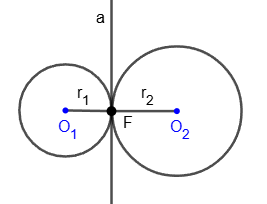
The formula for the distance between the centers of the circles is: O₁O₂ = r₁ + r₂.

Secant

A secant is a line that intersects a circle at two points.