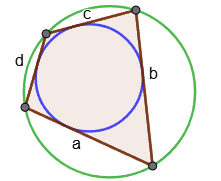
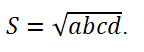Designations:
R - radius of the circumscribed circle;
r - radius of the inscribed circle;
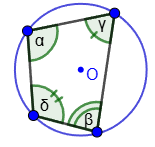
α, β, γ, δ - angles of the quadrilateral;
a, b, c, d - sides of the quadrilateral;
S - area of the quadrilateral.
Quadrilaterals inscribed in a circle. Circles circumscribed around a quadrilateral.
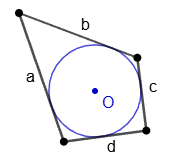
A quadrilateral is called inscribed in a circle if the circle passes through all four vertices of the quadrilateral. The circle in this case is called circumscribed around the quadrilateral.
1. A quadrilateral can be inscribed in a circle if and only if the sums of the opposite angles are equal to 180 degrees: α+β = γ+δ = 180
∘.
2. Ptolemy's Theorem.
For an inscribed quadrilateral, the product of the lengths of the diagonals is equal to the sum of the products of the lengths of two pairs of its opposite sides AC*BD = AB*CD + BC*AD.
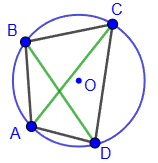
Converse theorem.
If the product of the lengths of the diagonals of a quadrilateral is equal to the sum of the products of the lengths of two pairs of its opposite sides, then such a quadrilateral can be inscribed in a circle.
3. A circle can be described
- about a parallelogram if and only if this parallelogram is a rectangle;
- about a rhombus if and only if this rhombus is a square;
- about a trapezoid if and only if the trapezoid is isosceles.
4. Brahmagupta's formula for the area of an inscribed quadrilateral with semiperimeter
p = (a+b+c+d)/2:
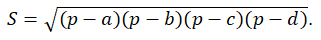
 2. Ptolemy's Theorem.
2. Ptolemy's Theorem. Converse theorem.
Converse theorem.
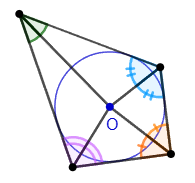 5. The formula for the area of a circumscribed quadrilateral through the radius of the inscribed circle and the sides of the quadrilateral:
5. The formula for the area of a circumscribed quadrilateral through the radius of the inscribed circle and the sides of the quadrilateral: