Triangles inscribed in a circle and circumscribed about a circle

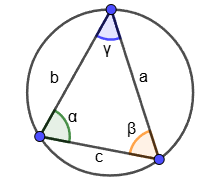
Designations:
R - radius of the circumscribed circle;
r - radius of the inscribed circle;
α, β, γ - angles of the triangle;
a, b, c - sides of the triangle;
S - area of ​​the triangle.

Triangles inscribed in a circle. Circles circumscribed around a triangle.

A triangle is called inscribed in a circle if the circle passes through all three vertices of the triangle. The circle in this case is called circumscribed around the triangle. A circle can be circumscribed around any triangle.

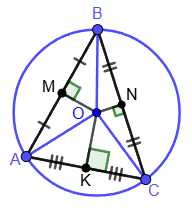
1. The center of the circle circumscribed around the triangle lies at the intersection of the median perpendiculars:

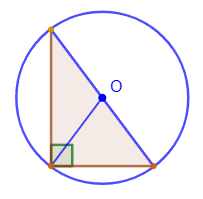
2. The center of the circle circumscribed around a right triangle lies in the middle of the hypotenuse, and its radius is equal to half of the hypotenuse.

3. The formula for the area of an inscribed triangle in terms of the radius of the circumscribed circle and the sides of the triangle:

S = abc/(4R).

4. The sine theorem:

a/sinα = b/sinβ = c/sinγ = 2R.

Triangles circumscribed around a circle. Circles inscribed in triangles.

A triangle is called circumscribed around a circle if the circle touches all three sides of the triangle. The circle in this case is called inscribed in the triangle. A circle can be inscribed in any triangle.

1. The center of the circle inscribed in the triangle lies at the intersection of bisectors:

2. The radius of the circle inscribed in a right triangle with cathetes a, b and hypotenuse c is equal to:

r = ½(a+b-c).

3. The formula for the area of a circumscribed triangle in terms of the radius of the inscribed circle and the sides of the triangle:

S = ½(a+b+c)*r.