Angles between chords, tangents and secants
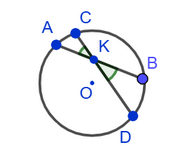
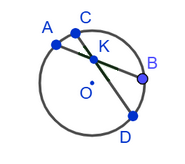
1. The vertical angles between intersecting chords are equal to half the sum of the magnitudes of the arcs enclosed between their sides: ∠AKC = ∠BKD = ½(∪AC + ∪BD).
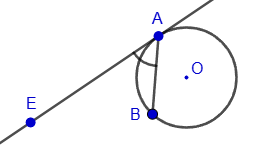
2. The angle between a tangent and a chord coming from one point on a circle is half of the magnitude of the arc between them: ∠BAE = ½(∪AB).
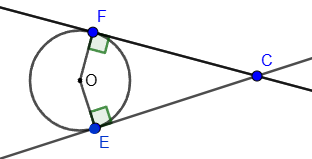
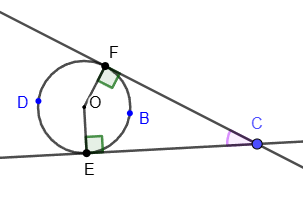
3. The angle between two tangents coming from the same point is equal to the half difference of the magnitudes of the arcs enclosed between its sides: ∠FCE = ½(∪FDE - ∪FBE).
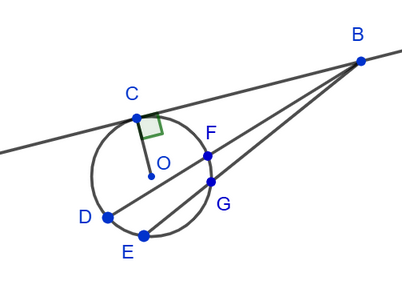
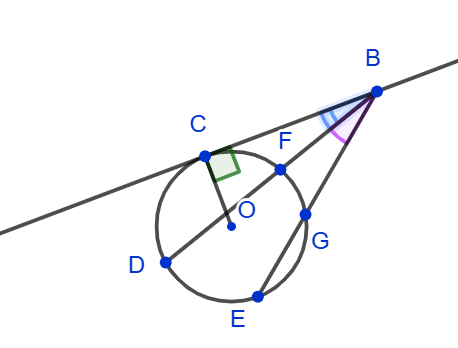
4. The angle between the tangent and the secant coming from the same point is equal to the half difference of the magnitudes of the arcs enclosed between its sides: ∠DBC = ½(∪CD - ∪CF).
The angle between two secants originating from the same point is equal to the half-difference of the magnitudes of the arcs enclosed between its sides: ∠DBE = ½(∪DE - ∪FG).
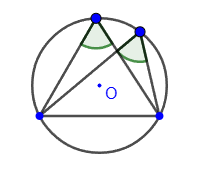
5. If two equal angles rest on the same segment, a circle can be drawn through the vertices of the angles and the ends of the segment:
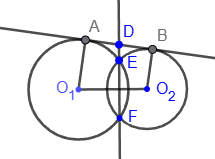
 2. A diameter perpendicular to a chord divides it in half: BD⊥EF => EA = AF.
2. A diameter perpendicular to a chord divides it in half: BD⊥EF => EA = AF.
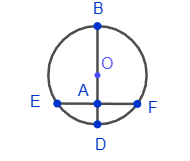 3. The midpoint perpendicular to the chord passes through the center of the circle: EA = AF, BD⊥EF => центр O∈BD.
3. The midpoint perpendicular to the chord passes through the center of the circle: EA = AF, BD⊥EF => центр O∈BD. 4. The segments of tangents coming from one point are equal: CF = CE.
4. The segments of tangents coming from one point are equal: CF = CE.