Basic theorems about segments

Thales' theorem

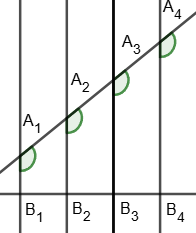
1. Parallel lines that intersect two given lines and cut off equal segments on one line, cut off equal segments on the other line:

A₁A₂ = A₂A₃ = A₃A₄ ⇔ B₁B₂ = B₂B₃ = B₃B₄.

Theorem on proportional segments

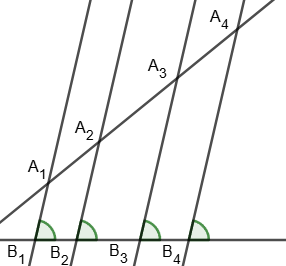
2. Parallel lines that intersect two given lines and cut off proportional segments on one line also cut off proportional segments on the other line:

A₁A₂ : A₂A₃ : A₃A₄ = B₁B₂ : B₂B₃ : B₃B₄.

Ceva's theorem

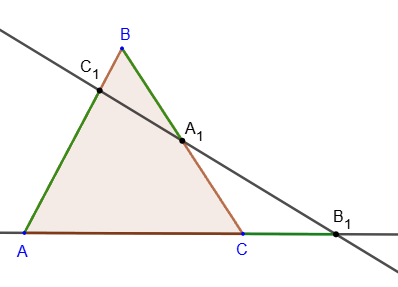
3. If points A₁, B₁, C₁ lie respectively on sides BC, AC, AB of triangle ABC, and segments AA₁, BB₁ and СC₁ intersect at one point, then the equality is true:

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1.

Ceva's converse theorem

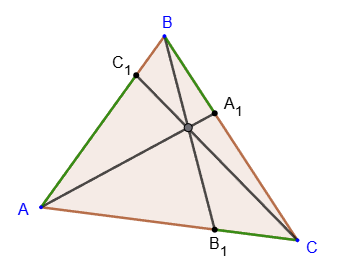
4. If points A₁, B₁, C₁ lie respectively on sides BC, AC, AB of triangle ABC, and

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1,

then the segments AA₁, BB₁ and СC₁ intersect at one point.

Menelaus' Theorem

5. If points A₁, B₁, C₁ lie respectively on sides BC, AC, AB of triangle ABC or on their extensions, then the equality is true:

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1.

The converse of Menelaus' theorem

6. If in triangle ABC the points A₁, B₁, C₁ lie respectively on sides BC, AC, AB or on their extensions, and for these points the equality is valid

(AC₁ ∕ C₁B) * (BA₁ ∕ A₁C) * (CB₁ ∕ B₁A) = 1,

then points A₁, B₁, C₁ lie on the same line.