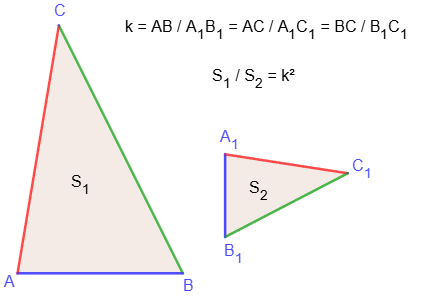
Similar triangles
If triangles ABC and A
1B
1C
1 have respectively equal angles:
∠A = ∠A1, ∠B = ∠B1, ∠C = ∠C1,
then the sides lying opposite the equal angles are called similar:
AB and A1B1, BC and B1C1, CA and C1A1.
Two triangles whose angles are equal and pairs of similar sides are proportional are called similar.
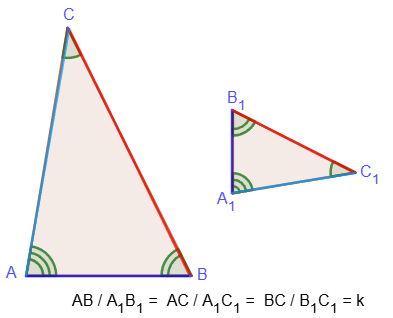
In this case, the proportionality coefficient k is called the similarity coefficient.
Signs of similarity of triangles
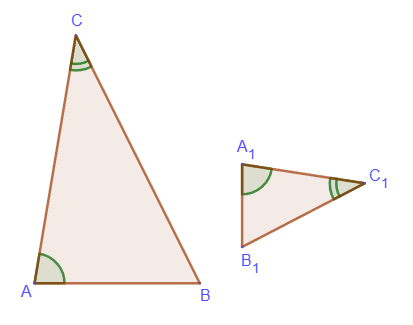
1. If two angles of one triangle are equal to two angles of another triangle, then such triangles are similar.
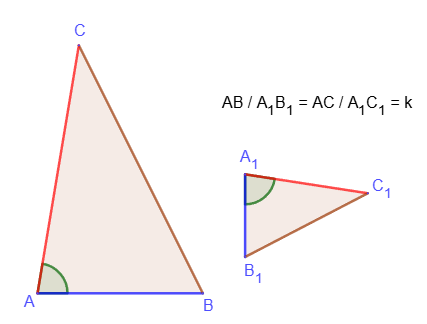
2. If two sides of one triangle are proportional to two sides of another triangle and the angles between these sides are equal, then such triangles are similar.
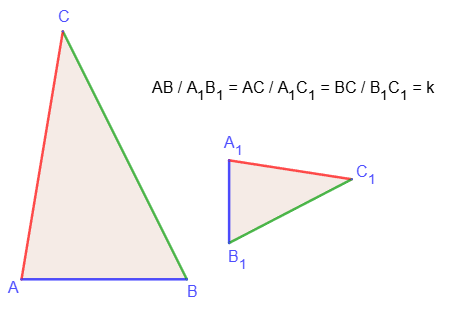
3. If the sides of one triangle are proportional to the sides of another triangle, then such triangles are similar.
Ratio of areas of similar triangles
The areas of similar triangles are related as the coefficient of similarity squared.
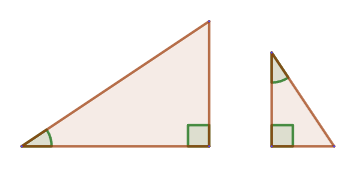
Signs of similarity of rectangular triangles
1. If the acute angle of one rectangular triangle is equal to the acute angle of another rectangular triangle, then such triangles are similar.
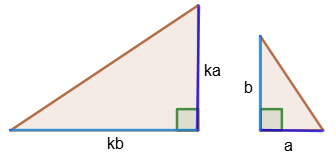
2. If two legs of one rectangular triangle are proportional to two legs of another rectangular triangle, then such triangles are similar.
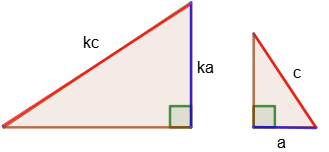
3. If the leg and hypotenuse of one rectangular triangle are proportional to the leg and hypotenuse of another rectangular triangle, then such triangles are similar.
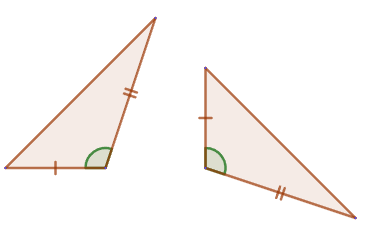 2. If the side and the two angles adjacent to it of one triangle are equal to the side and the two angles adjacent to it of another triangle, then such triangles are equal.
2. If the side and the two angles adjacent to it of one triangle are equal to the side and the two angles adjacent to it of another triangle, then such triangles are equal.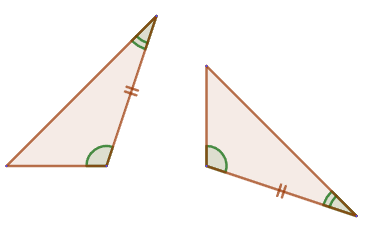 3. If three sides of one triangle are equal to three sides of another triangle, then such triangles are equal.
3. If three sides of one triangle are equal to three sides of another triangle, then such triangles are equal.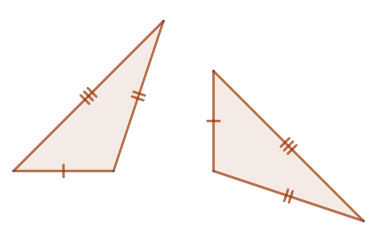
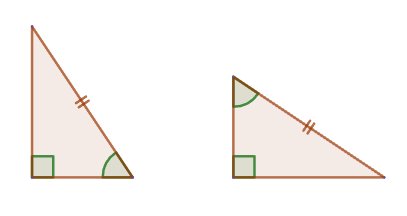
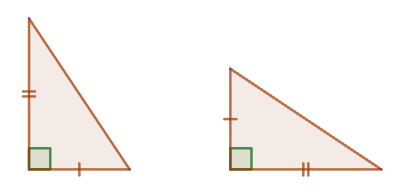 2. If the leg and hypotenuse of one rectangular triangle are respectively equal to the leg and hypotenuse of another rectangular triangle, then such triangles are equal.
2. If the leg and hypotenuse of one rectangular triangle are respectively equal to the leg and hypotenuse of another rectangular triangle, then such triangles are equal.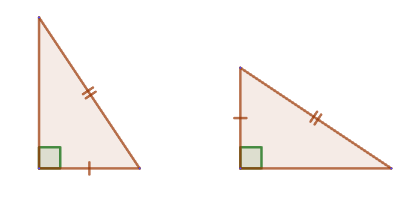 3. If the leg and acute angle of one rectangular triangle are respectively equal to the leg and acute angle of another rectangular triangle, then such triangles are equal.
3. If the leg and acute angle of one rectangular triangle are respectively equal to the leg and acute angle of another rectangular triangle, then such triangles are equal.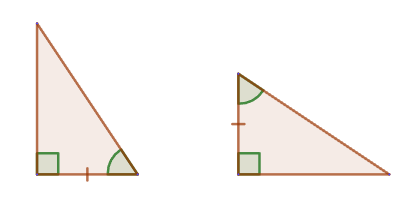
 In this case, the proportionality coefficient k is called the similarity coefficient.
In this case, the proportionality coefficient k is called the similarity coefficient. 2. If two sides of one triangle are proportional to two sides of another triangle and the angles between these sides are equal, then such triangles are similar.
2. If two sides of one triangle are proportional to two sides of another triangle and the angles between these sides are equal, then such triangles are similar. 3. If the sides of one triangle are proportional to the sides of another triangle, then such triangles are similar.
3. If the sides of one triangle are proportional to the sides of another triangle, then such triangles are similar.

 2. If two legs of one rectangular triangle are proportional to two legs of another rectangular triangle, then such triangles are similar.
2. If two legs of one rectangular triangle are proportional to two legs of another rectangular triangle, then such triangles are similar. 3. If the leg and hypotenuse of one rectangular triangle are proportional to the leg and hypotenuse of another rectangular triangle, then such triangles are similar.
3. If the leg and hypotenuse of one rectangular triangle are proportional to the leg and hypotenuse of another rectangular triangle, then such triangles are similar.