Vector addition
1. Addition of any two vectors according to the triangle rule.
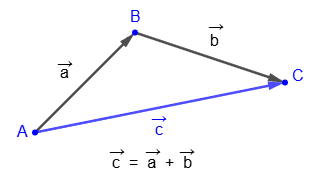
To add two vectors
and
,
we set aside vector
from any point on the plane, and vector
from the end point of vector
.
Then the sum of vectors is called a vector
with the beginning at the initial point of vector
and the end point at the end point of the vector
:
Thus, vector
shows the displacement of the end point of vector
as a result of adding vector b to it.
.
If we denote vectors by two letters, we obtain the rule for adding two vectors
and
in letter form:
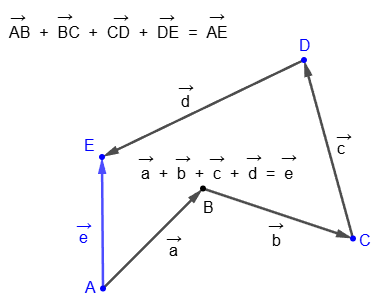
If we generalize this result to the sum of several vectors, we obtain the polygon rule for adding any number of vectors: the sum of several vectors is a vector with a beginning at the initial point of the first vector and an end at the end point of the last vector:
2. Addition of two non-collinear vectors using the parallelogram rule.
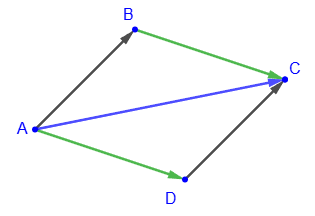
If we plot two non-collinear vectors
and
from one point A of the plane and construct a parallelogram ABCD on these vectors, then the sum of the vectors ABCD,
and
will be the vector
(the diagonal of the parallelogram), because
. Really,
 Thus, vector shows the displacement of the end point of vector as a result of adding vector b to it. .
If we denote vectors by two letters, we obtain the rule for adding two vectors and in letter form:
If we generalize this result to the sum of several vectors, we obtain the polygon rule for adding any number of vectors: the sum of several vectors is a vector with a beginning at the initial point of the first vector and an end at the end point of the last vector:
Thus, vector shows the displacement of the end point of vector as a result of adding vector b to it. .
If we denote vectors by two letters, we obtain the rule for adding two vectors and in letter form:
If we generalize this result to the sum of several vectors, we obtain the polygon rule for adding any number of vectors: the sum of several vectors is a vector with a beginning at the initial point of the first vector and an end at the end point of the last vector:
 2. Addition of two non-collinear vectors using the parallelogram rule.
2. Addition of two non-collinear vectors using the parallelogram rule.
 If we plot two non-collinear vectors and from one point A of the plane and construct a parallelogram ABCD on these vectors, then the sum of the vectors ABCD,
and will be the vector (the diagonal of the parallelogram), because
. Really,
If we plot two non-collinear vectors and from one point A of the plane and construct a parallelogram ABCD on these vectors, then the sum of the vectors ABCD,
and will be the vector (the diagonal of the parallelogram), because
. Really,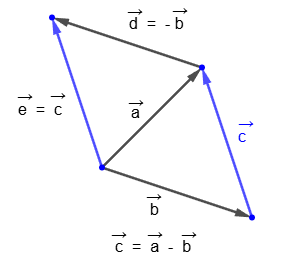
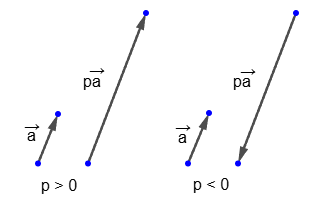 From the definition of multiplication of a vector by a number it follows that
From the definition of multiplication of a vector by a number it follows that