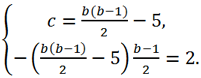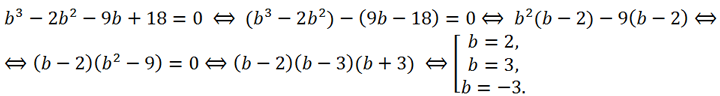Example 2.
Find the real roots of the equation -2x
3 + 3x
2 - 4x - 9 = 0.
Solution.
The divisors of the free term are the numbers: ±1, ±3, ±9. The divisors of the higher coefficient are the numbers: ±1, ±2.
This means that the roots of the original equation can be among the numbers: ±1, ±3, ±9,
.
A simple substitution shows that -1 is the root of the equation. Using Horner's scheme, we divide the left side of the original equation by x + 1.
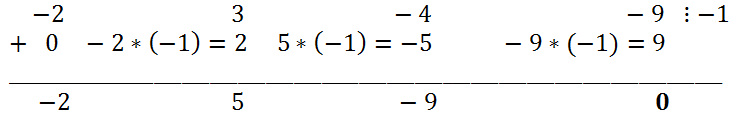
Thus, -2x
3 + 3x
2 - 4x - 9 = (x + 1)(-2x
2 + 5x - 9). Therefore, the original equation is equivalent to (x + 1) (-2x
2 + 5x - 9)=0. Solving the quadratic equation -2x
2 + 5x - 9 = 0, we obtain, that its discriminant is < 0, therefore, it has no real roots.
Answer: -1.
Example 3.
Solve the equation 2x
3 - x
2 - 8x + 4 = 0.
Solution.
The divisors of the free term are the numbers: ±1, ±2, ±4. The divisors of the higher coefficient are the numbers: ±1, ±2.
This means that the roots of the original equation can be among the numbers: ±1, ±2, ±4.
A simple substitution shows that 2 is the root of the equation. Using Horner's scheme, we divide the left side of the original equation by x - 2.
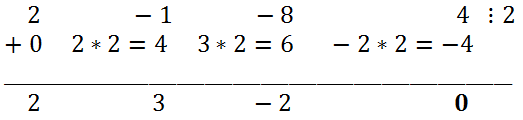
Thus, 2x
3 - x
2 - 8x + 4 = (x - 2)(2x
2 + 3x - 2). Therefore, the original equation is equivalent to (x - 2) (2x
2 + 3x - 2) = 0. Solving the quadratic equation 2x
2 + 3x - 2 = 0, we get,
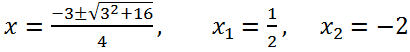 Answer:
Answer: -2,
, 2.
Another way to factorize a polynomial of the third degree is the method of indefinite coefficients. It is quite cumbersome, but sometimes it is very useful when solving various kinds of problems, and not only in the case of factorization. The factorization of any polynomial of the third degree can be represented as follows a(x) = (x-x
0)*(a
0x
2 + bx + c).
Opening the brackets, we get a(x) = a
0x
3 + x
2(b - a
0x
0) + x*(c - bx
0) - cx
0.
Now equating the coefficients for the same powers of x and the free terms in the original polynomial and in the polynomial a(x), we get a system of four equations and four unknowns a
0, b, c and x
0. Let's consider the application of the method of undefined coefficients using examples.
Example 4.
Solve the equation x
3 + 2x
2 - 5x - 6 = 0.
Solution.
Since any polynomial of degree 3 can be represented as a
0x
3 + x
2(b - a
0x
0) + x*(c - bx
0) - cx
0, then equating the coefficients for the same degrees of x, we obtain the following system of equations:
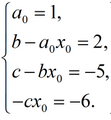
Or
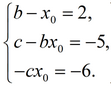
We find from the first equation x
0 = b - 2 and substitute it into the remaining two. We get
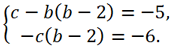
Now let's find the variable c from the first equation and substitute it into the second.
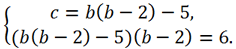
By opening the brackets in the second equation and solving it, we find b:
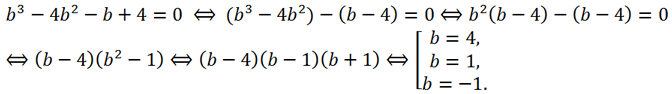
If b=4, then c=3, x
0 = 2. Therefore, x
3 + 2x
2 - 5x - 6 = (x - 2)(x
2 - 4x + 3)=(x - 2)(x + 1)(x + 3).
If b = 1, then c = -6, x
0 = -1. Therefore, x
3 + 2x
2 - 5x - 6 = (x + 1)(x
2 + x - 6)=(x + 1)(x + 3)(x - 2).
If b = -1, then c = -2, x
0 = -3. Therefore, x
3 + 2x
2 - 5x - 6=(x + 3)(x
2 - x - 2) = (x + 3)(x - 2)(x + 1).
Thus, the original equation is equivalent to the equation (x + 3)(x - 2)(x + 1) = 0.
Equating each of the factors to zero, we obtain the roots of the equation x = -3, x = 2, x = -1.
Answer: -3, -1, 2.
Example 5.
Solve the equation 2x
3 + x
2 - 5x + 2 = 0.
Solution.
By equating the corresponding coefficients for the same powers of x, we obtain the following system of equations:
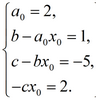
Or
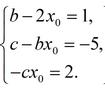
We find from the first equation x
0 =
and substitute it into the remaining two. We get
Now let's find the variable c from the first equation and substitute it into the second.
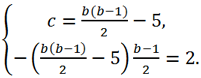
Multiplying the left and right sides of the second equation by 4 and opening the brackets, we find b:
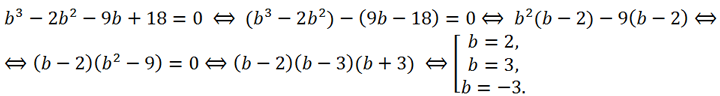
If b=2, then c=-4, x
0 =
. Hence, 2x
3 + x
2 - 5x + 2 = (x -
)(2x
2 + 2x - 4) = 2(x -
)(x - 1)(x + 2).
If b = 3, then c = -2, x
0 = 1. Therefore, 2x
3 + x
2 - 5x + 2 = (x - 1)(2x
2 + 3x - 2)=2(x - 1)(x -
)(x + 2).
If b = -3, then c = 1, x
0 = -2. Therefore, 2x
3 + x
2 - 5x + 2 = (x + 2)(2x
2 - 3x + 1) = 2(x + 2)(x -
)(x - 1).
Therefore, the original equation is equivalent to the equation 2(x + 2)(x -
)(x - 1) = 0.
Equating each of the factors to zero, we obtain the roots of the equation x = -2, x =
, x = 1.
Answer: -2,
, 1.
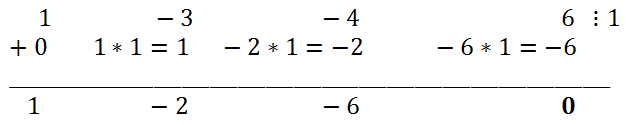
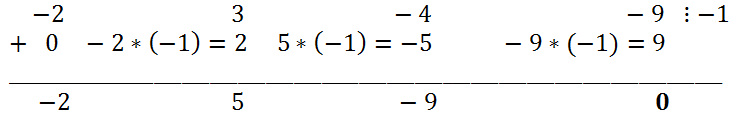
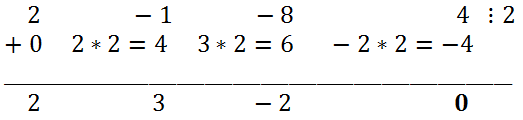
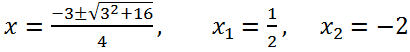
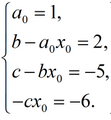 Or
Or
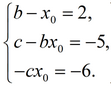 We find from the first equation x0 = b - 2 and substitute it into the remaining two. We get
We find from the first equation x0 = b - 2 and substitute it into the remaining two. We get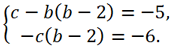
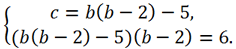
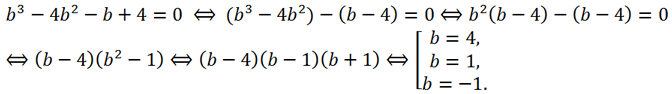
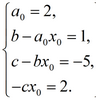 Or
Or 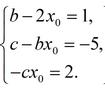 We find from the first equation x0 =
We find from the first equation x0 =