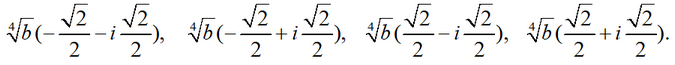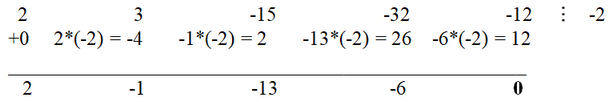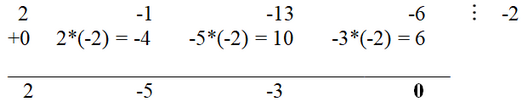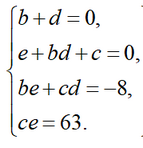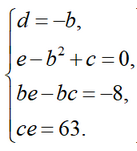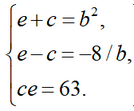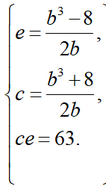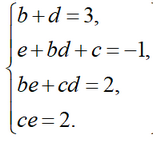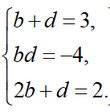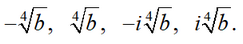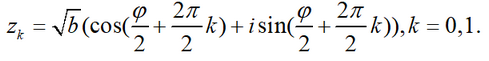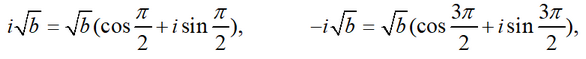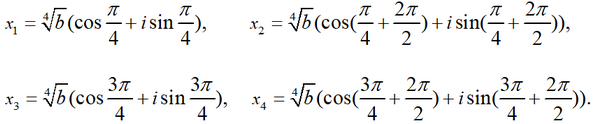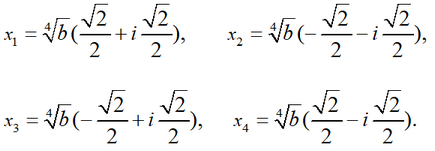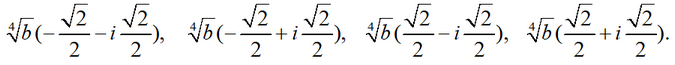Solving equations of the fourth degree by factorization

According to the fundamental theorem of algebra, quartic equation always has 4 roots (taking into account multiplicity). For equations with real coefficients, if the root of the equation is a complex number, then the complex conjugate will also be its root. Thus, a polynomial of the fourth degree with real coefficients a(x) = a₀*x⁴ +a₁*x³ + a₂*x² + a₃*x + a₄, a₀ ≠ 0, can always be represented as the product of its highest coefficient a₀ and several polynomials with real coefficients: linear ones of the form x-x₀ corresponding to its real roots, and quadratic ones of the form x² + bx + c corresponding to products of conjugate complex roots.
Equating each factor in the expansion to zero, we will find all the roots of the equation. Let's consider the solution of equations of the fourth degree by the method of factorization using examples.

Examples of solving quartic equations using the factorization method

Example 1.
Solve the equation 2x⁴ + 3x³ - 15x² - 32x - 12 = 0.
Solution.
The divisors of the free term are the numbers: ±1, ±2, ±3, ±4, ±6, ±12. The integer roots of the equation must be sought among them. A simple substitution shows that the root of the equation is the number -2. Therefore, the original equation is equivalent to (x + 2)*(2x³ + bx² + cx + d) = 0.
To find the polynomial 2x³ + bx² + cx + d, you need to divide the left side of the original equation by x+2. To divide a polynomial by a binomial, we will use Horner's scheme.


Thus, 2x⁴ + 3x³ - 15x² - 32x - 12 =  (x + 2)(2x³ - x² - 13x - 6). Therefore, the original equation is equivalent to

(x + 2)(2x³ - x² - 13x - 6)= 0.

We solve the cubic equation 2x³ - x² - 13x - 6 = 0 in the same way .
By substitution we see that -2 is also a root of a cubic equation, Therefore, -2 is a root of multiplicity 2. Again we use Horner's scheme to divide by x+2:


It remains to solve the resulting quadratic equation 2x² - 5x² - 3 = 0. Its roots:
Answer: -2, -1/2 , 3.

Example 2.
Solve the equation x⁴ - 8x + 63 = 0.
Solution.
Let's try to factor the left side of the equation into 2 quadratic factors: x⁴ - 8x + 63 = (x² + bx + c)(x² + dx + e).
We will find the unknown values ​​b, c, d, e using the method of undetermined coefficients. We multiply two brackets and equate the coefficients at the same powers of x, we get the following system of equations:
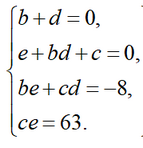
Let us express the unknown d through b and substitute it into the equations of the system:
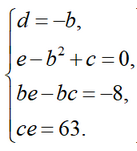
Hence
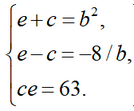
Adding and subtracting the first two equations of the system, we obtain expressions for e and c through b:
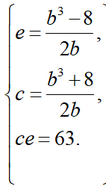
Finally, substituting the expressions for e and c into the third equation, we obtain an equation for b

b⁶ - 63*4*b² - 64 = 0.

By simple substitution we see that b=4 is the root of the equation. Therefore, d = -4, e = 7, c = 9. Thus, we obtain the factorization

x⁴ - 8x + 63 =(x² + 4x + 9)(x² - 4x + 7).

By equating each bracket to zero and solving the resulting quadratic equations, we find solutions to the original equation:

x_1,2 = -2±i√5;     x_3,4 = 2±i√3.

Answer: -2-i√5, -2+i√5, 2-i√3, 2+i√3.

Another example of the application of the method of undetermined coefficients.
Example 3. Solve the equation x⁴ + 3x³ - x² + 2x + 2 = 0.
Solution.
Let's try to factor the left side of the equation into 2 quadratic factors: x⁴ +3x³ - x² + 2x + 2 = (x² + bx + c)(x² + dx + e).
We multiply two brackets and equate the coefficients at the same powers of x, we get the following system of equations:
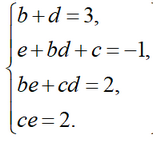
Since ce=2, then if we assume that c and e are integers, then there are 2 possible options c=±2, since the option c=±1 simply changes the order of the quadratic factors. It is easy to verify that the solution of the system exists only when e=2, then c=1. Substituting these values ​​into the system, we obtain
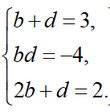
Hence b = -1, d = 4. Thus, we obtain the factorization

x⁴ +3x³ - x² + 2x + 2 = (x² - x + 1)(x² + 4x + 2).

By equating each bracket to zero and solving the resulting quadratic equations, we find solutions to the original equation:

x_1,2 = (1±i√3)/2;     x_3,4 = -2±√2.

Answer: -2-√2, -2+√2, (1-i√3)/2, (1+i√3)/2.

Example 4.
Solve the equation x⁴ - b = 0, where b≥0.
Solution.
Let's factor the left side of the equation using the difference of squares formula:

(x² -√b)(x² +√b) = 0.

Equating each bracket to zero, we get x² = √b or x² = √-b.
Hence
Answer: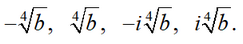

Example 5.
Solve the equation x⁴ + b = 0, where b≥0.
Solution.
Let's factor the left side of the equation using the difference of squares formula:

(x² -√(-b))(x² +√(-b)) = 0  or   (x² -i√b)(x² +i√b) = 0.

Equating each bracket to zero, we get

x² = i√b   or   x² = -i√b.

As is known, the second root of a complex number z,

z = r *(cosφ + isinφ)

has 2 complex values √z=z_k , k=0,1, where
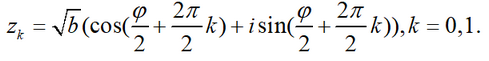
Since
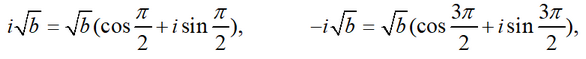
for the square roots of i√b and -i√b we obtain the expressions
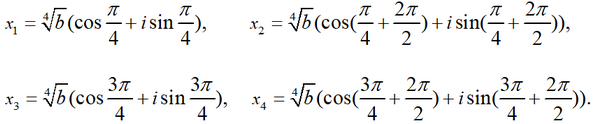
Hence taking into account that cos(π/4)=√2/2, sin(π/4)=√2/2, cos(3π/4)=-√2/2, sin(3π/4)=√2/2, we obtain the final expressions for the roots of the original equation:

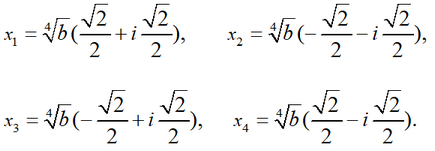Answer: