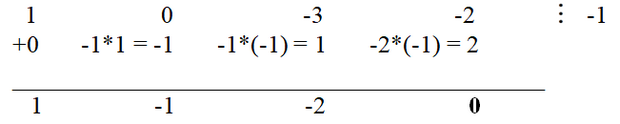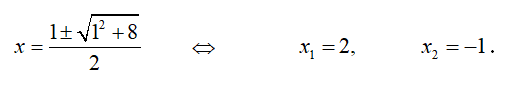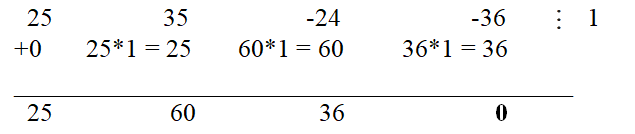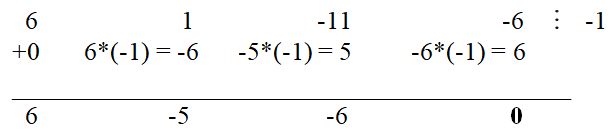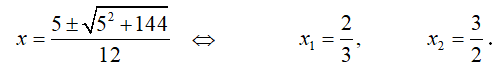Factorization of a third degree polynomial

Polynomial of degree 3 a(x) = a₀*x³ + a₁*x² + a₂*x+ a₃, a₀ ≠ 0, always has 3 roots (taking into account multiplicity). If a complex number is the root of a polynomial, then the complex conjugate will also be its root, therefore, a cubic polynomial always has at least one real root. Consider the factorization of polynomials of the third degree using examples.

Examples of factorization of a polynomial of the third degree

Example 1.
Factorize a polynomial x³ - 3x - 2.
Solution.
Divisors of the free term: ±1, ±2. This means that the roots of the polynomial must be searched among them. A simple substitution shows that the root of the polynomial is the number -1. This means that the original polynomial must be divided by x+1.
Let's use Horner's scheme:


Thus, x³ - 3x - 2= (x + 1)(x² - x - 2). To find the remaining 2 roots of the polynomial, we solve the quadratic equation x² - x - 2 = 0:

Hence, x³ - 3x - 2 = (x + 1)(x² - x - 2) = (x + 1)²(x - 2).
Answer: x³ - 3x - 2= (x + 1)²(x - 2).

Example 2.
Factorize a polynomial 25x³ + 35x² - 24x - 36.
Solution.
Divisors of the free term: ±1, ±2, ±3, ... .
Divisors of the leading coefficient: ±1, ±5, ±25.
This means that we will look for the roots of the original polynomial among the numbers: ±1, ±2, ±3, ... , ±1/2,  ±1/5; ... . Again, by simple substitution we verify that 1 is the root of the polynomial. Using the Horner's scheme, we divide the original polynomial by x - 1:


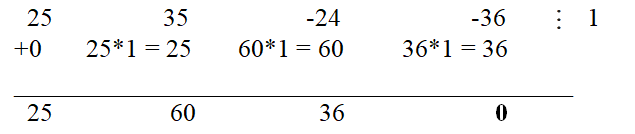
Thus, 25x³ + 35x² - 24x - 36= (x + 1)(25x² + 60x + 36). But a square trinomial 25x² + 60x + 36 = (5x + 6)².
Answer: 25x³ + 35x² - 24x - 36= (x - 1)(5x + 6)².

Example 3.
Factorize a polynomial 6x³ + x² - 11x - 6.
Solution.
A simple substitution shows that -1 is a root of the polynomial. Using Horner's scheme, we divide the original polynomial by x + 1:


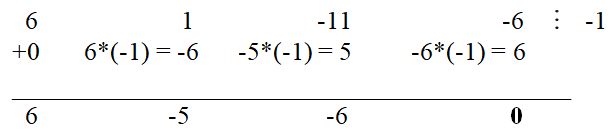
Solving a quadratic equation 6x² - 5x - 6 = 0, we get,


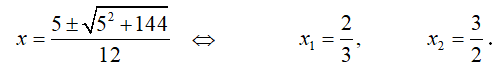
Hence, 6x² - 5x - 6 = 6(x - 2/3)(x - 3/2). Thus, 6x³ + x² - 11x - 6 = 6(x + 1)(x - 2/3)(x - 3/2).
Answer: 6x³ + x² - 11x - 6 = (x + 1)(3x - 2)(2x - 3).