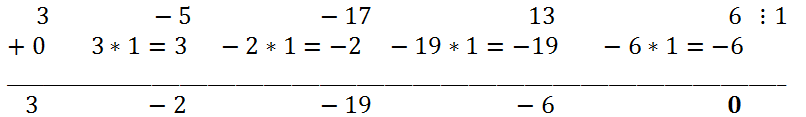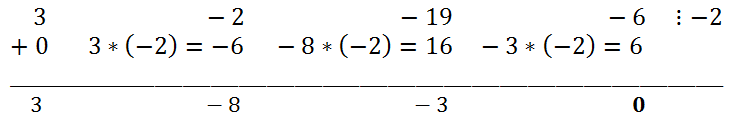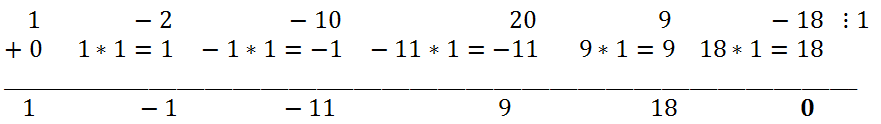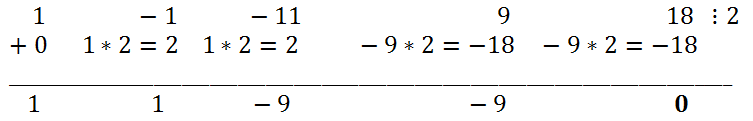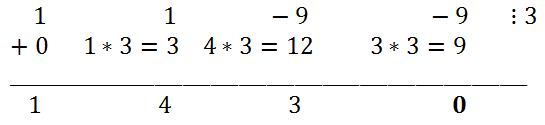Examples of factorization of polynomials
Example 1.
Factorize a polynomial 3x
4 - 5x
3 - 17x
2 + 13x + 6.
Solution.
A fourth degree polynomial can have at most 4 different roots. Let's try to find these roots.
Divisors of the free member: ±1, ±;2, ±3, ±6.
Divisors of the leading coefficient: ±1, ±3.
Therefore, rational roots of a polynomial can be sought among the numbers ±1, ±;2, ±3, ±6,
.
Substituting x = 1 into the polynomial, we see that x = 1 is the root of the polynomial. This means that the original polynomial must be divided by x-1. Let's use
Horner's scheme.
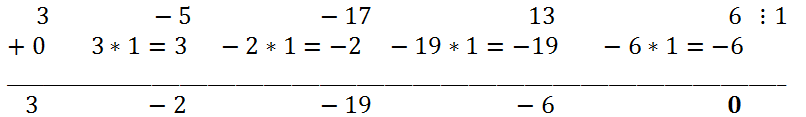
So, 3x
4 - 5x
3 - 17x
2 + 13x + 6=(x - 1)(3x
3 - 2x
2 - 19x - 6).
Now we need to factorize the polynomial 3x
3 - 2x
2 - 19x - 6.
Divisors of the free member: ±1, ±;2, ±3, ±6.
Divisors of the leading coefficient: ±1, ±3.
That is, its rational roots can be sought among the same numbers as the roots of the original polynomial:
±1, ±;2, ±3, ±6,
.
Substituting x = -2 into the polynomial, we see that x = -2 is the root of the polynomial. This means that the original polynomial must be divided by x + 2.
Let's use Horner's scheme again.
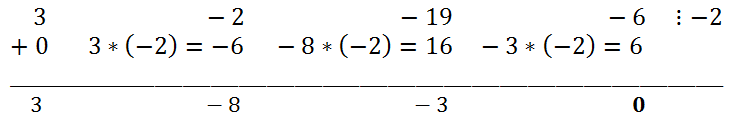
Therefore, 3x
3 - 2x
2 - 19x - 6 = (x + 2)(3x
2 - 8x - 3). Let's try to lower the degree of the polynomial 3x
2 - 8x - 3 in the same way, although we can simply solve the quadratic equation.
Divisors of the free member: ±1, ±;2, ±3.
Divisors of the leading coefficient: ±1, ±3.
That is, its rational roots can be sought among numbers ±1, ±;2, ±3,
. We check by substitution that the numbers are suitable
and 3. All roots have been found, which means the factorization has also been found:
3x
4 - 5x
3 - 17x
2 + 13x + 6 = 3(x - 1)(x + 2)(x - 3)(x + 1/3).
Answer: 3x
4 - 5x
3 - 17x
2 + 13x + 6 = (x - 1)(x + 2)(x - 3)(3x + 1).
Example 2.
Factorize a polynomial x
5 - 2x
4 - 10x
3 + 20x
2 + 9x - 18.
Solution.
A fifth-degree polynomial can have at most 5 different roots. Let's try to find these roots. Since the divisor of the leading coefficient is 1, rational roots of the polynomial can be sought among the divisors of the free term: ±1, ±;2, ±3, ±6, ±9, ±18. Substituting x = 1 into the polynomial, we see that x = 1 is a root of the polynomial. This means that the original polynomial must be divided by x-1. Let's use Horner's scheme.
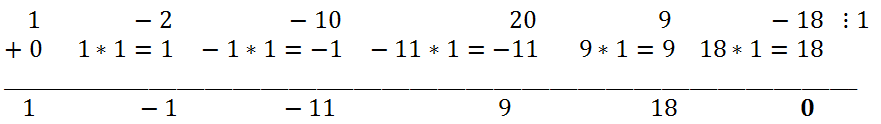
So, x
5 - 2x
4 - 10x
3 + 20x
2 + 9x - 18 = (x - 1)(x
4 - x
3 - 11x
2 + 9x + 18). Similarly, the rational roots of the polynomial x
4- x
3- 11x
2 + 9x + 18 can be sought among the same divisors of the free term: ±1, ±;2, ±3, ±6, ±9, ±18. Substituting x=2 into the polynomial, we see that x=2 is a root of the polynomial. This means that this polynomial must be divided by x-2.
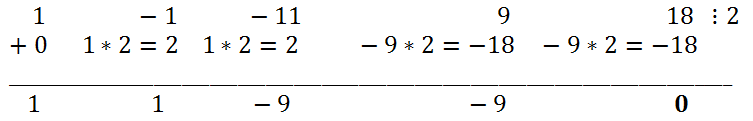
Thus, x
4 - x
3 - 11x
2 + 9x + 18 = (x - 2)(x
3 + x
2 - 9x - 9). The roots of a polynomial x
3 + x
2 - 9x - 9 can be found among the divisors of the free term 9:±1, ±3, ±9. It is easy to see that x = 3 is a root of the polynomial. Let us lower the degree of this polynomial by dividing it by x-3.
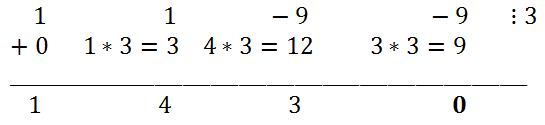
Hence, x
3 + x
2 - 9x - 9 = (x - 3)(x
2 + 4x + 3). The roots of the square trinomial x
2+ 4x + 3 are the numbers -1 and -3. The process of finding the roots of the original polynomial is complete.
Answer: x
5 - 2x
4 - 10x
3 + 20x
2 + 9x - 18 = (x - 1)(x + 1)(x - 2)(x - 3)(x + 3).
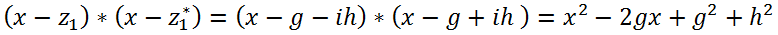 is a quadratic expression.
is a quadratic expression.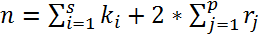 That is, if all the roots of a polynomial with real coefficients are known, then we can immediately write its factorization.
That is, if all the roots of a polynomial with real coefficients are known, then we can immediately write its factorization.