Angles

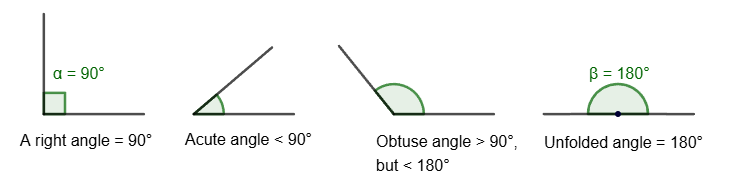
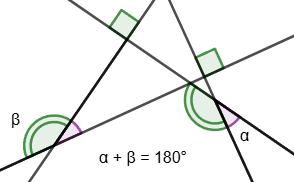Types of angles

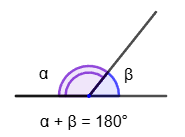
Adjacent and vertical angles

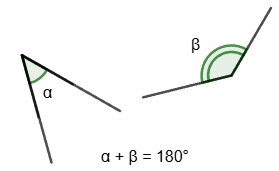
1. Two angles are called adjacent if they have one common side and the other two lie on the same line. Since these angles add up to a straight angle, the sum of adjacent angles is 180^∘.

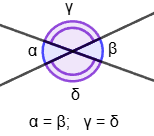
2. Two angles are called vertical if the sides of one angle are continuations of the sides of the other. Pairs of vertical angles: α and β; γ and δ. The vertical angles are equal to each other.

Angles at the intersection of two lines by a third

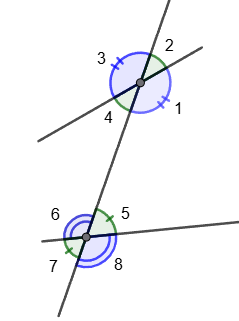
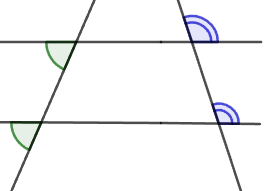
3. Crosswise lying angles:
pairs of interior angles lying crosswise ∠1 and ∠6; ∠4 and ∠5;
pairs of external crosswise lying angles ∠2 and ∠7; ∠3 and ∠8.

4.One-sided angles: pairs of internal one-sided angles ∠1 and ∠5; ∠4 and ∠6;
pairs of external one-sided angles ∠2 and ∠8; ∠3 and ∠7.

5. Corresponding angles:
pairs of corresponding angles ∠1 and ∠8; ∠2 and ∠5; ∠3 and ∠6; ∠4 and ∠7.

Parallelism of two lines

6. If, when two lines intersect by a third line, the angles lying crosswise are equal, then such lines are parallel. If two lines are parallel, then when they intersect by a third line, the angles lying crosswise are equal.


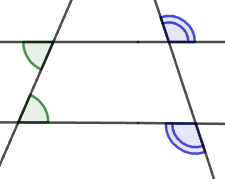
7. If, when two lines intersect by a third line, the sum of one-sided angles is equal 180^∘, then such lines are parallel. If two lines are parallel, then when they intersect by third line, the sum of one-sided angles is equal 180^∘.


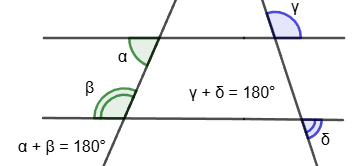
8. If, when two lines intersect by a third line, the corresponding angles are equal, then such lines are parallel. If two lines are parallel, then when they intersect by a third line, the corresponding angles are equal.

Angles with correspondingly parallel or perpendicular sides

9. Angles with correspondingly parallel sides are equal if they are both acute or both obtuse.

10. The sum of angles with correspondingly parallel sides is 180^∘, if one of them is acute and the other is obtuse.

11. Angles with correspondingly perpendicular sides are equal if they are both acute or both obtuse.
12. The sum of angles with correspondingly perpendicular sides is 180^∘, if they are both acute or both obtuse.

Angle bisector. Angles between bisectors

The bisector of an angle is a ray that divides the angle in half.

13. The angle formed by the bisectors of adjacent angles is equal 90^∘.


14. The angle formed by the bisectors of the one-sided angles of a parallelogram is equal to 90^∘.

15. The angle formed by the bisectors of the one-sided angles at the lateral sides of the trapezoid is equal to 90^∘.