A trapezoid is a quadrilateral with two parallel sides and two non-parallel sides:
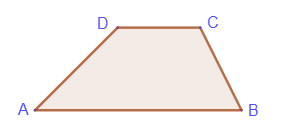
The parallel sides of a trapezoid are called bases (AB - lower base, CD - upper base), and the non-parallel sides AD and BC are called lateral sides.
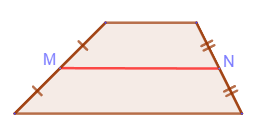
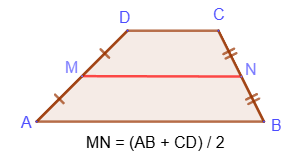
The midline of a trapezoid is a segment that connects the midpoints of the lateral sides of the trapezoid:
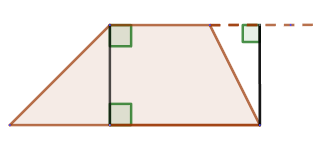
The height of a trapezoid is the perpendicular dropped from any point on one of the bases of the trapezoid to the other base or its extension:
Types of trapezoids
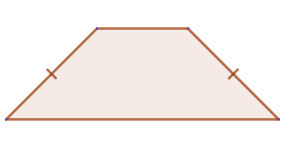
1. A trapezoid is called isosceles if its lateral sides are equal:
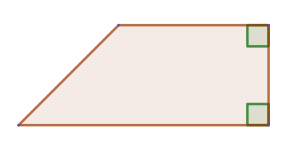
2. A trapezoid is called a right-angled trapezoid if one of its angles is a right angle:
Properties of a trapezoid
1. The midline of a trapezoid is parallel to its bases and equal to their half-sums:
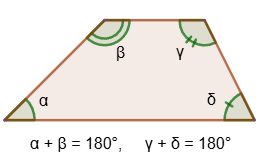
2. The sum of the angles adjacent to the lateral side of a trapezoid is 180°:
3. Triangles formed by the intersection of diagonals and containing bases are
similar:
ΔAOB∾ΔCOD, k = AB/CD=AO/OC=BO/OD
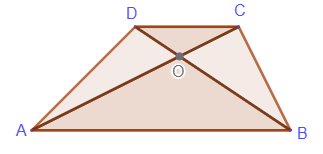
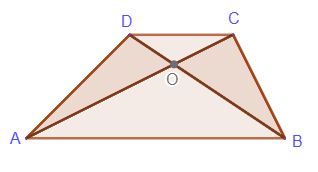
4. Triangles formed by the intersection of diagonals and containing lateral sides have equal areas:
SΔADC=SΔBCD, SΔADO=SΔBCO, SΔADB=SΔBCA
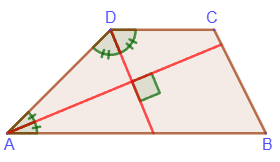
5. The
bisectors of the angles at the lateral side of the trapezoid are perpendicular:
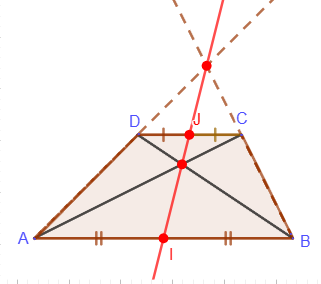
6. The intersection point of the diagonals of a trapezoid, the intersection point of the extensions of its lateral sides and the midpoints of the bases lie on the same line:
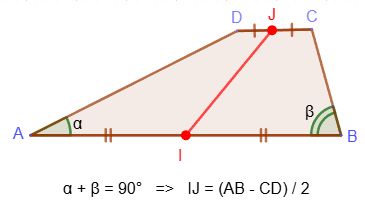
7. If the sum of the angles at any base of the trapezoid is equal to 90°, then the segment connecting the midpoints of the bases is equal to their half-difference:
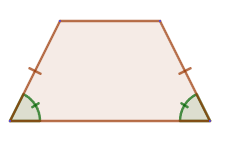2. If the diagonals of an isosceles trapezoid are perpendicular, then the height is equal to half the sum of the bases: DH=(AB+CD)/2.
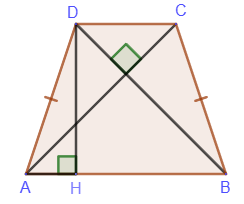3. If the trapezoid is isosceles, then a circle can be described around it: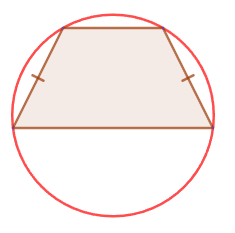
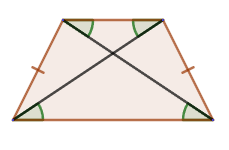3. If a circle can be described around a trapezoid, then it is isosceles.
