Equation of a line on a plane

General equation of a straight line on a plane

The general equation of a straight line on a plane is a first-degree equation with two unknowns:

Ax + By + C = 0,

where A and B are not equal to 0 simultaneously.
If A=0, and B≠0, By+C=0 ⇔ y=-C/B - is the equation of a straight line parallel to the OX axis.
If A≠0, and B=0, Ax+C=0 ⇔ x=-C/A - is the equation of a straight line parallel to the OY axis.
If С=0, Ax + By = 0 is the equation of a straight line passing through the origin (0,0).

Let's find the coordinates of the points of intersection of the straight line with the coordinate axes.
If y=0, then x=-C/A, therefore, the point (-C/A; 0) - is the intersection point with the OX axis.
If x=0, then y=-C/B, therefore, the point (0; -C/B) - is the intersection point with the OY axis.

Equation of a straight line with an angular coefficient

From the general equation of a straight line

Ax + By + C = 0

you can express y if B≠0:

y = - A ∕ B ⋅ x - C ∕ B.

Thus, the equation of a straight line can be represented as

y = kx + b, wrere k = - A ∕ B, b = - C ∕ B.

The coefficient k is called the angular coefficient, because k sets the angle α of inclination of a straight line.

k = tgα.

Here, α - is the angle between the positive direction of the OX axis and a straight line, measured counterclockwise. The equation of a straight line with an angular coefficient defines any straight line other than a straight line parallel to the OY axis. Let us consider the cases of the location of a straight line depending on the values of the parameters k and b.
1) If we substitute x=0 into the equation with the angular coefficient, we get y=b. Therefore, the line y = kx + b always passes through a point with coordinates (0,b). In other words, the straight line intersects the OY axis at (0,b). If b=0, then the equation takes the form y=kx, and the line passes through the origin, the point (0,0).
If b>0, then the straight line intersects the OY axis in the upper half-plane, if b<0, then in the lower.
2) If α=0, then k=tgα=0, and equation of the straight line takes the form y=b. Its graph is a straight line parallel to the OX axis. If k=0, b=0, the line coincides with the OX axis.
If α - acute angle, then k=tgα>0, and the equation y=kx+b defines an increasing function.
If α - obtuse angle, then k=tgα<0, and the equation y=kx+b defines a decreasing function.

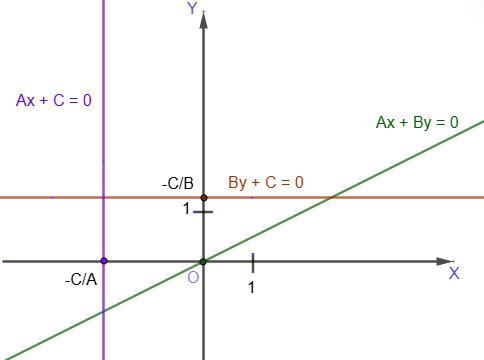
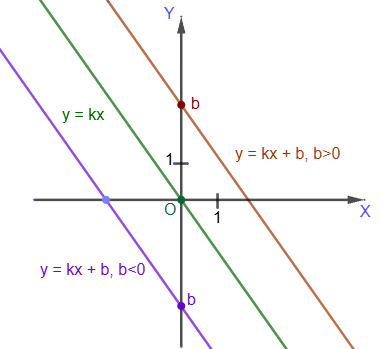
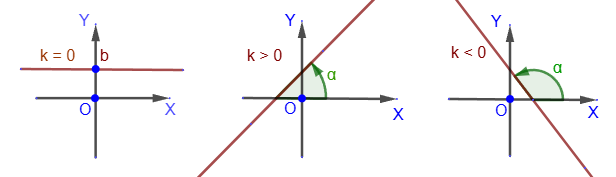
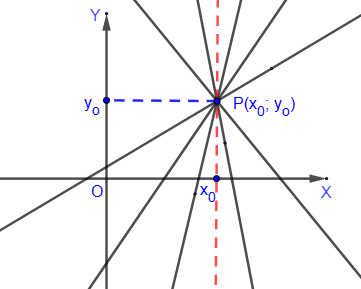
Equation of a straight line passing through a given point

Let a point P(x₀; y₀) be given. Let's substitute the coordinates of point P into the equation of the line y=kx+b:

y₀ = kx₀ + b   ⇔    b = y₀ - kx₀.

Substituting the found value of b into the equation, we obtain:

y = kx + y₀ - kx₀   ⇔   y = k(x - x₀) + y₀   ⇔   y - y₀ = k(x - x₀).

This equation of a straight line defines a sheaf of straight lines (except a vertical straight line) with center at point P(x₀; y₀):

The equation of a straight line passing through two given points

Let two points be given P₁(x₁; y₁) and P₂(x₂; y₂). We obtain the equation of a straight line passing through these points.
Equation of a sheaf of lines with center at a point P₁(x₁; y₁):

y - y₁ = k(x - x₁).

To obtain from this equation the equation of a straight line passing through the point P₂(x₂; y₂), you need to find the corresponding angular coefficient. To do this, simply substitute the coordinates of point P₂ into the sheaf equation:

y₂ - y₁ = k(x₂ - x₁)   ⇔   k = (y₂ - y₁) ∕ (x₂ - x₁).

And finally, we get

y - y₁ = (y₂ - y₁) ∕ (x₂ - x₁)⋅(x - x₁).

Usually, the equation of a straight line passing through two points is written as:

(y - y₁) ∕ (y₂ - y₁) = (x - x₁) ∕ (x₂ - x₁).

In this case, the angular coefficient of the straight line k = (y₂ - y₁) ∕ (x₂ - x₁).
If the given points P₁ and P₂ lie on lines parallel to the coordinate axes, that is y₂ = y₁ ( || axes OX) or x₂ = x₁ ( || axes OY), the equations of the lines will be, respectively, y = y₁ or x = x₁.

Conditions of parallelism and perpendicularity of two straight lines

1) Two straight lines y=k₁x+b₁ and y=k₂+b₂ are parallel if and only if their angular coefficients coincide k₁=k₂.
2) We obtain the condition of line perpendicularity. Consider two straight lines with angular coefficients k₁=tgα₁ and k₂=tgα₂. A necessary and sufficient condition for their perpendicularity:

α₁ - α₂ = π/2   ⇔   α₁ = α₂+π/2   ⇔   tgα₁ = tg(α₂+π/2)   ⇔   tgα₁ = -ctgα₂ ⇔ k₁k₂ = -1.

Thus, we have obtained the necessary and sufficient condition for the perpendicularity of two straight lines: the product of the angular coefficients must be   -1.

Angle between two lines

Let us find the angle α between two straight lines AC and BC, given by the equations y=k₁x+b₁, y=k₂+b₂. We assume that the lines are not perpendicular.
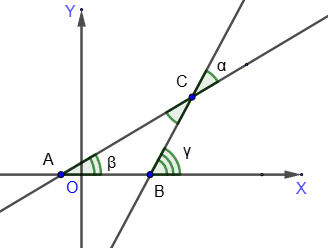
Angle ∠ACB=∠α, since these angles are vertical. Since the angle γ is an external angle of a triangle ABC,

γ = α + β ⇔ α = γ - β.

Therefore, using the well-known trigonometric formula, we obtain:

tgα = tg(γ - β)   ⇔   tgα = (tgγ - tgβ) ∕ (1 + tgγ tgβ).

Since tgβ = k₁, tgγ = k₂,

tgα = (k₁ - k₂) ∕ (1 + k₁k₂).

An angle between two lines is by definition an acute angle (or a right angle if the lines are perpendicular), therefore, tgα≥0. Therefore, the formula for the tangent of the angle between lines is:

tgα = |(k₁ - k₂) ∕ (1 + k₁k₂)|.

If lines AC and BC are perpendicular, then k₁k₂=-1, and in this case the formula does not make sense.
Also, the formula does not make sense if at least one of the lines is parallel to the OY axis. In this case, the angle between the lines is easy to find for common sense reasons using the formula α=|π/2-β| or α=|π/2-γ|.

A condition under which three given points lie on the same line

Let three points be given P₁(x₁; y₁), P₂(x₂; y₂) and P₃(x₃; y₃). Let's write the equation of a straight line passing through two points P₁ and P₂:

(y - y₁) ∕ (y₂ - y₁) = (x - x₁) ∕ (x₂ - x₁).

For the point P₃ to lie on this straight line, it is necessary and sufficient that its coordinates satisfy this equation. Therefore, we simply substitute the coordinates x₃, y₃ of the point P₃ into the equation of the straight line and obtain the condition under which three points lie on the same straight line:

(y₃ - y₁) ∕ (y₂ - y₁) = (x₃ - x₁) ∕ (x₂ - x₁).