Rhombus
A rhombus is a
parallelogram with all sides equal.
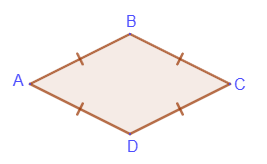
Properties of a rhombus
1. The diagonals of a rhombus are the
bisectors of its angles and intersect at right angles:
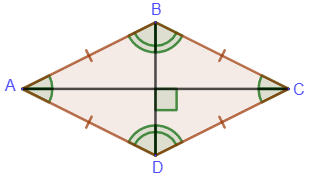
In addition, a rhombus has all the properties of a parallelogram:
2. The opposite sides of a rhombus are parallel.
3. Opposite angles of a rhombus are pairwise equal.
4. The sum of the one-sided angles of the rhombus is equal 180°.
5. The diagonals of a rhombus intersect and are divided in half by the point of intersection.
Signs of a rhombus
1. If a parallelogram has two adjacent sides that are equal, then it is a rhombus.
2. If the diagonals of a parallelogram are mutually perpendicular, then this parallelogram is a rhombus.
3. If the diagonal of a parallelogram is the bisector of its angle, then this parallelogram is a rhombus.
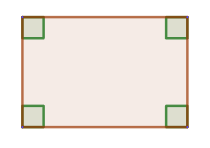
Square
A square is a rectangle with all sides equal. From the definition of a square it follows that a square is a rhombus. Therefore, a square has all the properties of a rectangle and a rhombus.
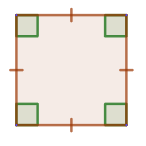
Properties of a square
1. All angles of a square are right angles.
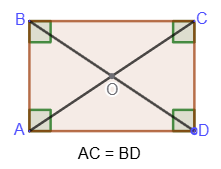
2. The diagonals of a square are equal: AC=BD.
3. The diagonals of a square are the
bisectors of its angles and intersect at right angles.
4. The diagonals of a square intersect and are divided in half by the point of intersection: AO=OC=BO=OD.
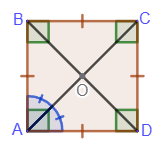
Signs of a square
1. If the diagonals of a rhombus are equal, then the rhombus is a square.
2. If the diagonals of a rectangle are mutually perpendicular, then the rectangle is a square.
3. If one of the diagonals of a rectangle is the bisector of any of its angles, then the rectangle is a square.
