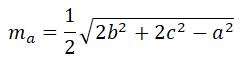Bisector of a triangle
The bisector of a triangle is a segment of the
bisector of an angle of a triangle that connects the vertex of the triangle to a point on the opposite side.
1. The bisectors of any triangle intersect at one point.
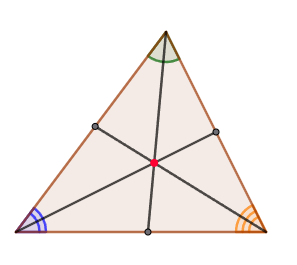
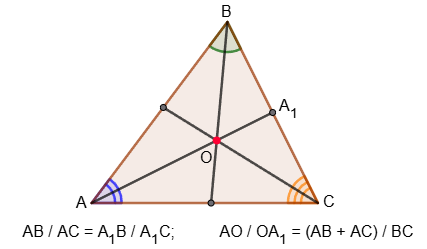
2. The bisector of an angle of a triangle divides the opposite side into parts proportional to the adjacent sides.
AB ∕ AC = A1B ∕ A1C.
3. In a triangle, the intersection point of the bisectors divides the bisector in the ratio
AO ∕ OA1=(AB+AC) ∕ BC.
4. The length of the bisector l
с, drawn to the side c of a triangle with sides a, b, c is equal to
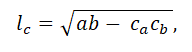
where c
a and c
b – segments into which the bisector divides the side c.
Median of a triangle
The median of a triangle is a segment that connects the vertex of the triangle with the midpoint of the opposite side.
5. The medians of any triangle intersect at one point.
6. In a triangle, the intersection point of the medians divides the medians in a ratio of 2:1, counting from the vertex.
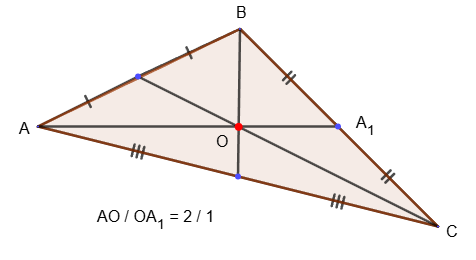
7. The length of the median m
a, drawn to the side a of a triangle with sides a, b, c is equal to
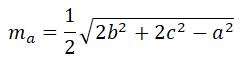
8. The median divides a triangle into two triangles of equal area.
9. Three medians divide a triangle into 6 triangles of equal area.


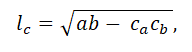 where ca and cb – segments into which the bisector divides the side c.
where ca and cb – segments into which the bisector divides the side c.