Coordinates of the sum and difference of vectors
Let the vectors be given
{x
1,y
1} and
{x
2,y
2}:
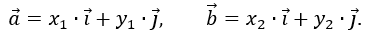
Let's find the coordinates {x,y} of the vector
, используя геометрическое определение суммы векторов:
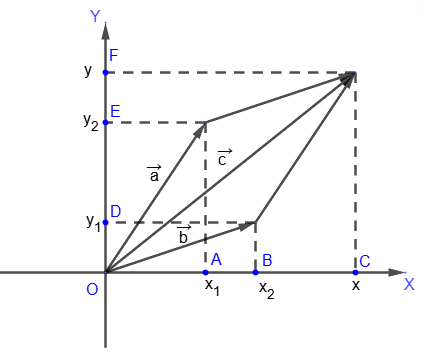
Since AC=OB and DF=OE, then x = x
1 + x
2, y = y
1 + y
2. Thus, the coordinates of the sum of two vectors are equal to the sum of the corresponding coordinates of these vectors.
You can derive these formulas using the properties of vector addition and vector multiplication by a number:
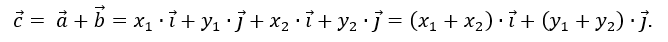
Obviously, to find the coordinates of the sum of several vectors, you need to add up the corresponding coordinates of these vectors.
In a similar way, formulas for the coordinates of the difference of two vectors are obtained
.
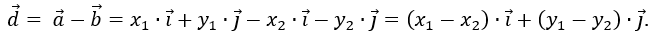
The coordinates of the difference of two vectors are equal to the difference of the corresponding coordinates of these vectors.
Coordinates of the vector, if the coordinates of its start and end points are given
Let the coordinates of the initial point A(x
1, y
1) of the vector
and the end point B be given B(x
2, y
2).
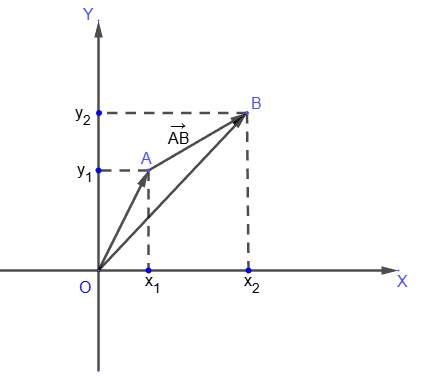
Since
,then the vector
has coordinates
{x2 - x1, y2 - y1}.
Thus, to find the coordinates of the vector
, we must subtract the corresponding coordinates of the initial point from the coordinates of the end point of the vector, and the formula for calculating its modulus is:
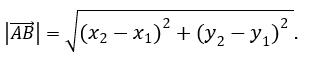
Coordinates of the product of a vector by a number
The coordinates of the product of a vector
{x, y} by a number q are equal to the products of the corresponding coordinates by this number:
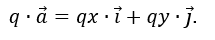
Therefore, the coordinates of the vector q⋅
{qx, qy}.
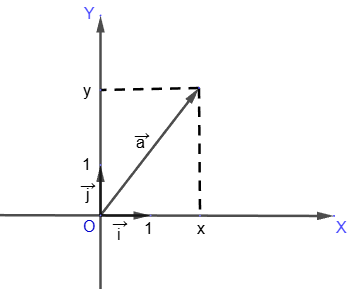 The decomposition of the zero vector can be represented as follows:
The decomposition of the zero vector can be represented as follows:
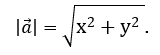
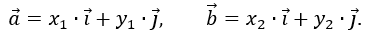 Let's find the coordinates {x,y} of the vector , используя геометрическое определение суммы векторов:
Let's find the coordinates {x,y} of the vector , используя геометрическое определение суммы векторов: Since AC=OB and DF=OE, then x = x1 + x2, y = y1 + y2. Thus, the coordinates of the sum of two vectors are equal to the sum of the corresponding coordinates of these vectors.
Since AC=OB and DF=OE, then x = x1 + x2, y = y1 + y2. Thus, the coordinates of the sum of two vectors are equal to the sum of the corresponding coordinates of these vectors.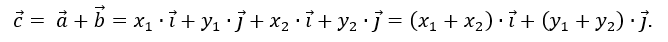 Obviously, to find the coordinates of the sum of several vectors, you need to add up the corresponding coordinates of these vectors.
Obviously, to find the coordinates of the sum of several vectors, you need to add up the corresponding coordinates of these vectors.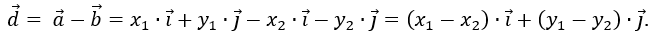 The coordinates of the difference of two vectors are equal to the difference of the corresponding coordinates of these vectors.
The coordinates of the difference of two vectors are equal to the difference of the corresponding coordinates of these vectors. Since ,then the vector has coordinates
Since ,then the vector has coordinates
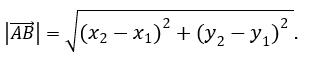
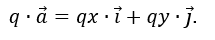 Therefore, the coordinates of the vector q⋅{qx, qy}.
Therefore, the coordinates of the vector q⋅{qx, qy}.