Coordinates of the middle of the segment
Let the segment AB be given: A=(x
1; y
1), B=(x
2; y
2). We need to find the coordinates (x; y) of its midpoint - point C.
From points A, B and C we drop perpendiculars onto the X-axis, they will intersect the X-axis at points E(x
1; 0), F(x
2; 0), G(x; 0), respectively.
According to
Thales' theorem, point G is the midpoint of segment EF, that is, EG=GF.
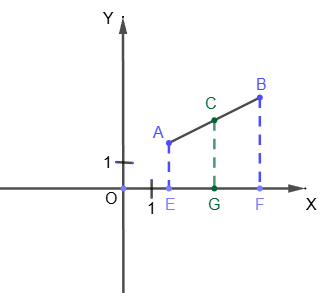
Therefore, x-x
1=x
2-x. From here we get the formula for the abscissa of the point G: x=(x
1+x
2)/2. This formula remains valid for all cases of the location of points A and B. Even if AB is parallel to OY, we simply get that the abscissas of points A, B, and C coincide.
To derive the formula for the ordinate of point C, we drop the perpendiculars from points A, B, and C onto the OY axis and similarly find that the ordinate y of point G is y=(y
1+y
2)/2.
Thus, the formulas for the coordinates of the middle of the segment have the form:
x=(x1+x2)/2, y=(y1+y2)/2.
The length of the segment, the distance between the points
Let the segment AB be given: A=(x
1; y
1), B=(x
2; y
2). We need to find its length, that is, the distance between points A and B.
From points A and B we drop perpendiculars to the X and Y axes. The line perpendicular to the X axis, passing through point A, intersects the line perpendicular to the Y axis, passing through point B, at point C=(x
1; y
2).
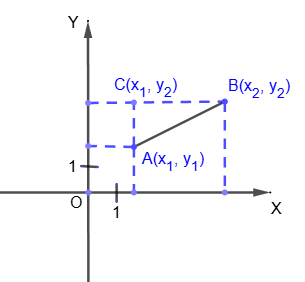
Thus, we get the right triangle ABC. We will find its hypotenuse AB using the
Pythagorean theorem:
AB2 = AC2 + BC2 <=> AB2 = (y2 - y1)2 + (x2 - x1)2
This formula is valid for any case of location of points A and B.
Thus, the square of the distance between two points A(x
1; y
1) and B(x
2; y
2) is determined by the formula:
AB2 = (y2 - y1)2 + (x2 - x1)2
 The abscissa of point A is the number x, the absolute value of which is equal to the distance from point A to the straight line OY. If point A is located in the right half-plane, then its abscissa x is a positive number, if in the left it is a negative number. If point A belongs to the OY axis, then x=0.
The abscissa of point A is the number x, the absolute value of which is equal to the distance from point A to the straight line OY. If point A is located in the right half-plane, then its abscissa x is a positive number, if in the left it is a negative number. If point A belongs to the OY axis, then x=0.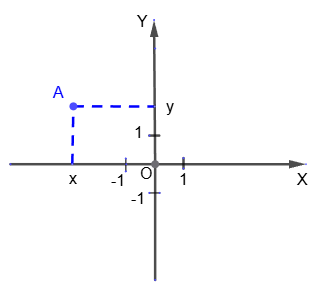
 Therefore, x-x1=x2-x. From here we get the formula for the abscissa of the point G: x=(x1+x2)/2. This formula remains valid for all cases of the location of points A and B. Even if AB is parallel to OY, we simply get that the abscissas of points A, B, and C coincide.
Therefore, x-x1=x2-x. From here we get the formula for the abscissa of the point G: x=(x1+x2)/2. This formula remains valid for all cases of the location of points A and B. Even if AB is parallel to OY, we simply get that the abscissas of points A, B, and C coincide. Thus, we get the right triangle ABC. We will find its hypotenuse AB using the Pythagorean theorem:
Thus, we get the right triangle ABC. We will find its hypotenuse AB using the Pythagorean theorem: