An equation of the form
ax2 + bx + c = 0, where
a, b, c – are some numbers, and
a ≠ 0, is called a quadratic equation. The polynomial
ax2 + bx + c is usually called a quadratic trinomial.
A quadratic equation is called complete if the coefficients
b and
c are nonzero.
An incomplete quadratic equation is an equation for which either
b = 0, or
= 0, or both
b = 0 and
c = 0 simultaneously. Therefore, incomplete quadratic equations have the form
ax2 = 0, or
ax2 + = 0, or
ax2 + bx = 0.
A reduced quadratic equation is an equation in which the coefficient
a = 1, that is, an equation of the form
x2 + px + q = 0.
Solving incomplete quadratic equations
Solving complete quadratic equations
Vieta's theorem and its application to solving quadratic equations
Solving of biquadratic equations
Examples of solving of quadratic equations
Example 1.Solve the quadratic equation
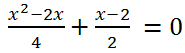 Solution.
Solution.
Let's bring the left side of the equation to a common denominator:
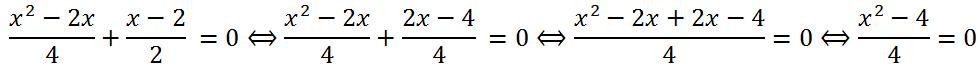
Multiply both parts of the equation by 4:
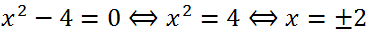 Answer:
Answer: -2, 2.
Example 2.Solve the quadratic equation x
2 + 3x + 10 = 0.
Solution.
Let's calculate the discriminant of the quadratic trinomial. We have a = 1, b = 3, c = 10.
D = b
2 - 4ac = 3
2 - 4*1*10 = 9 - 40 = -31 < 0, therefore, there are no real roots.
Answer: there are no roots.
Example 3.Solve the quadratic equation x
2 + 12x + 36 = 0.
Solution.
Let's calculate the discriminant of the quadratic trinomial. We have a = 1, b = 12, c = 36.
Since b = 12 is an even number, we calculate the discriminant D
1 :
D
1 = (
)
2 - ac = 6
2 - 1*36 = 0, therefore, the equation has a unique root
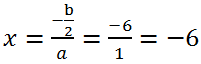
This equation can be solved without calculating the discriminant by converting the quadratic trinomial using the formula of reduced multiplication:
x
2 + 12x + 36 = 0 <=> (x + 6)
2 = 0 <=> x = -6.
Answer: -6.
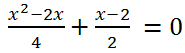 Solution.
Solution.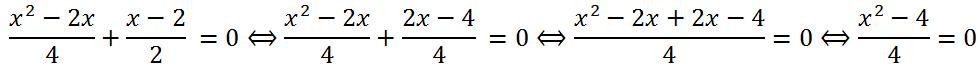
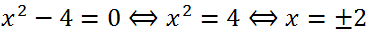
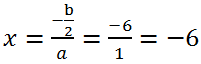 This equation can be solved without calculating the discriminant by converting the quadratic trinomial using the formula of reduced multiplication:
This equation can be solved without calculating the discriminant by converting the quadratic trinomial using the formula of reduced multiplication: