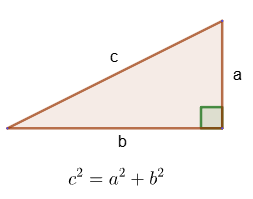
Pythagoras' theorem
5. In a rectangular triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.
From the Pythagorean theorem it follows that in any right triangle the hypotenuse is greater than each of the legs.
6. If the square of one side of a triangle is equal to the sum of the squares of the other two, then the triangle is rectangular.
A rectangular triangle with sides 3, 4, 5 is often called Egyptian.
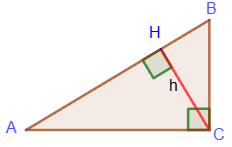
Projections of the legs on the hypotenuse
The segments into which
the base of the height of a right triangle, drawn from the vertex of the rectangular angle, divides the hypotenuse, are the projections of the legs onto the hypotenuse: AH - is the projection of the leg AC on the hypotenuse AB, BH - is the projection of the leg BC on the hypotenuse AB.
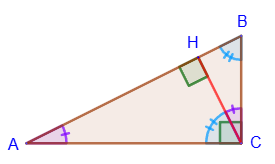
7. The height in a rectangular triangle drawn from the vertex of a right angle divides it into 2 triangles,
similar to given: ∆ ABC∼∆ ACH∼∆ CBH.
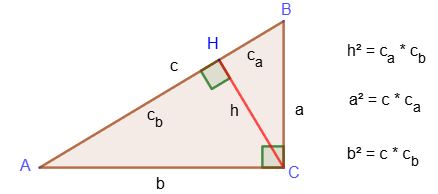
8. The square of the length of the height of a rectangular triangle drawn from the vertex of a right angle is equal to the product of the lengths of the projections of the legs on the hypotenuse.
9. The square of the length of the leg of a rectangular triangle is equal to the product of the hypotenuse and the length of the projection of this leg onto the hypotenuse.
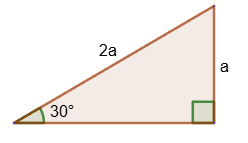 3. The median of a rectangular triangle, drawn from the vertex of the right angle, is equal to half the hypotenuse.
4. If the median of a triangle is equal to half the side to which it is drawn, then the triangle is rectangular.
3. The median of a rectangular triangle, drawn from the vertex of the right angle, is equal to half the hypotenuse.
4. If the median of a triangle is equal to half the side to which it is drawn, then the triangle is rectangular.
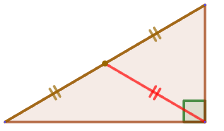

 7. The height in a rectangular triangle drawn from the vertex of a right angle divides it into 2 triangles, similar to given: ∆ ABC∼∆ ACH∼∆ CBH.
7. The height in a rectangular triangle drawn from the vertex of a right angle divides it into 2 triangles, similar to given: ∆ ABC∼∆ ACH∼∆ CBH.
 8. The square of the length of the height of a rectangular triangle drawn from the vertex of a right angle is equal to the product of the lengths of the projections of the legs on the hypotenuse.
9. The square of the length of the leg of a rectangular triangle is equal to the product of the hypotenuse and the length of the projection of this leg onto the hypotenuse.
8. The square of the length of the height of a rectangular triangle drawn from the vertex of a right angle is equal to the product of the lengths of the projections of the legs on the hypotenuse.
9. The square of the length of the leg of a rectangular triangle is equal to the product of the hypotenuse and the length of the projection of this leg onto the hypotenuse.
