A circle
A circle is a
geometrical locus of points, equidistant from one point - the center of the circle.
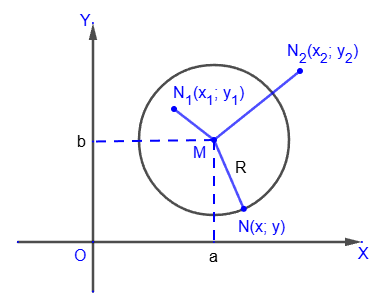
Let a point M with coordinates (a; b) be the center of a circle of
radius R, and let a point N(x; y) be any point on this circle. Then, by the definition of radius, R=MN.
Let the point N
1(x
1; y
1) lie inside the circle, the point N
2(x
2; y
2) lie outside the circle, and the point N(x; y) lies on the circle.
Equation of a circle
Using the formula for the
length of a segment, we get
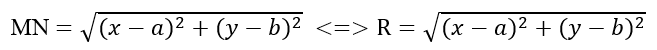
By squaring the last equation, we obtain the equation of a circle:
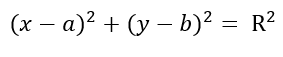
Only those points that belong to this circle satisfy this equation.
For example, the equation (x + 1)
2 + (y - 3)
2 = 25 defines a circle with center (-1;3) and radius R=√25=5.
If the center of the circle is at the origin, i.e. a=0, b=0, then the equation of the circle takes the form:
x2 + y2 = R2.
For example, the equation x
2 + y
2 = 8 defines a circle with its center at the origin (0;0) and radius R=√8=2√2.
Conditions for the location of a point relative to a circle
Let us consider a circle defined by the equation (x - a)
2 + (y - b)
2 = R
2.
If the point N
1(x
1; y
1) lies inside the circle, then the distance from the center (a; b) of the circle to this point is less than the radius of the circle. Therefore, if the condition
(x1 - a)2 + (y1 - b)2 < R2,
is true, then the point N
1 is located inside the circle.
If the point N
2(x
2; y
2) lies outside the circle, then the distance from the center of the circle to this point is greater than the radius of the circle. Therefore, if the condition
(x2 - a)2 + (y2 - b)2 > R2,
is true, then the point N
2 is located outside the circle.
If the condition
(x - a)2 + (y - b)2 = R2,
is true for the point N(x;y), then the point N(x;y) lies on the circle.

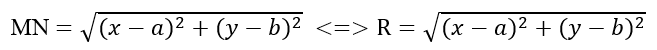 By squaring the last equation, we obtain the equation of a circle:
By squaring the last equation, we obtain the equation of a circle:
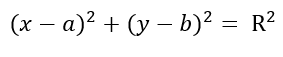 Only those points that belong to this circle satisfy this equation.
Only those points that belong to this circle satisfy this equation.