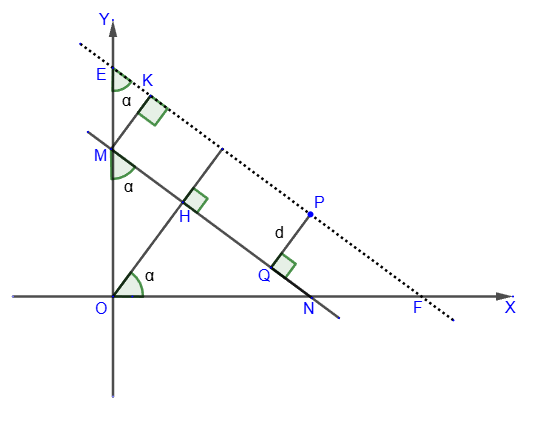
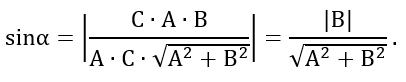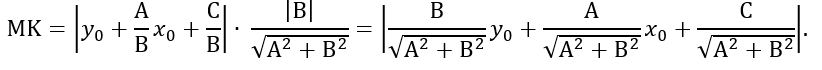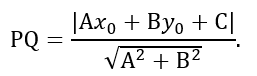Let us define an arbitrary point P(x
0; y
0) and a straight line MN: Ax + By + C = 0.
We obtain the formula for determining the distance d from the point P to the line MN. Let's write the equation of a straight line as an equation with an angular coefficient:
y = - A ∕ B ⋅ x - C ∕ B.
We find the coordinates of the points of intersection of this straight line with the coordinate axes:
M: x=0 => y = - C ∕ B => M(0; - C ∕ B).
N: y=0 => x = - C ∕ A => N(- C ∕ A; 0).
Let's draw a straight line EF || MN through the point P. Using the
equation of a straight line passing through a given point,
and the condition of
parallelism of straight lines, we obtain the equation of a straight line EF in the form:
y = - A ∕ B ⋅ x + y0 + A ∕ B ⋅ x0.
The distance between the parallel lines MN and EF is equal to the distance from the point P to the line MN, that is PQ=MK=d.
Let's ∠NOH=α, then ∠NOH=∠MEK=α, as
angles with respectively perpendicular sides.
Since ΔEKM - is rectangular, by definition the
sine of the angle is
sinα = MK / ME ⇔ MK = ME⋅sinα.
Coordinates of the point M(0;- C ∕ B), and of the point E(0; y
0 + A ∕ B ⋅ x
0), therefore, the
length of the segment ME is:
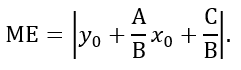
 We obtain the formula for determining the distance d from the point P to the line MN. Let's write the equation of a straight line as an equation with an angular coefficient:
We obtain the formula for determining the distance d from the point P to the line MN. Let's write the equation of a straight line as an equation with an angular coefficient:
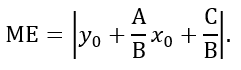
 The rectangular ΔMON is similar to the rectangular ΔHON, therefore,
The rectangular ΔMON is similar to the rectangular ΔHON, therefore,